Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 5
Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 5
Topic
Slope Formula
Description
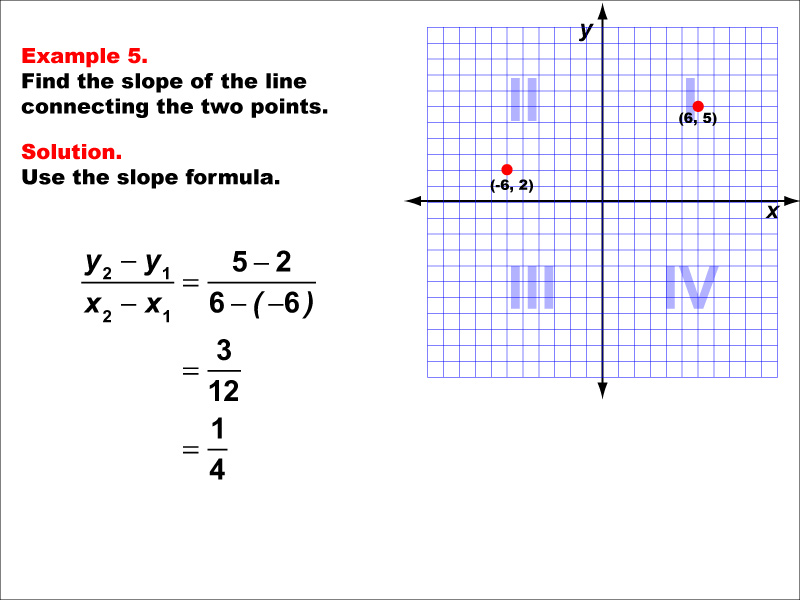
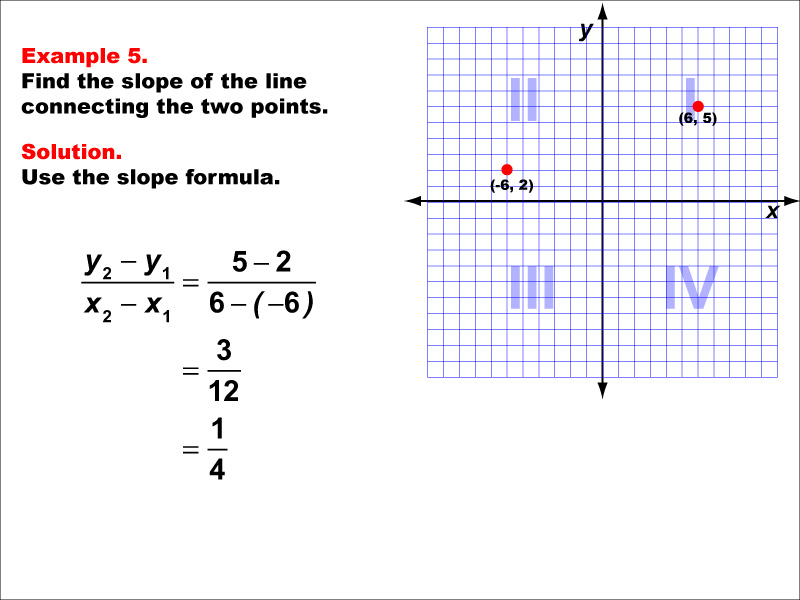
This example demonstrates the calculation of slope for a line connecting two points in different quadrants: (-6, -2) in Quadrant III and (6, 5) in Quadrant I. Applying the slope formula, we find that the slope is (5 - (-2)) / (6 - (-6)) = 7 / 12 = 1 / 4.
The slope formula is a crucial concept in coordinate geometry, helping us understand the steepness and direction of lines. This example shows how to handle negative coordinates and points in different quadrants when calculating slope.
By providing multiple examples like this, students can see how the slope formula applies in various scenarios, including those involving negative numbers and different quadrants. This helps reinforce the concept and improves their ability to calculate slopes accurately in more complex situations.
Teacher's Script: Let's examine this example closely. Notice how we handle the negative coordinates when calculating the slope. Remember, when subtracting a negative number, we actually add its positive value. In this case, the line has a positive slope, meaning it rises as we move from left to right. For every 4 units we move horizontally, the line rises by 1 unit.
For a complete collection of math examples related to Slope Formula click on this link: Math Examples: Slope Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.5, CCSS.MATH.CONTENT.7.RP.A.2.D |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Slope |
| Copyright Year | 2013 |
| Keywords | slope, rise over run, slope formula |