Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 6
Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 6
Topic
Slope Formula
Description
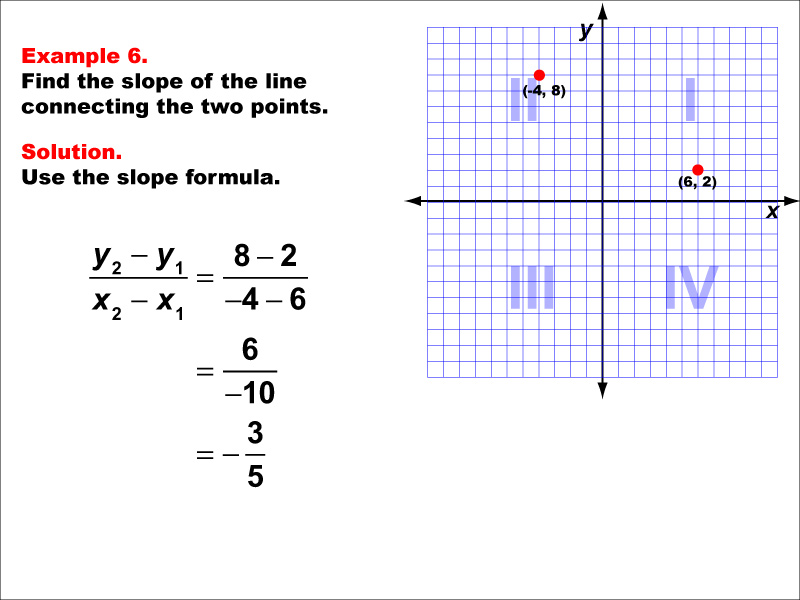
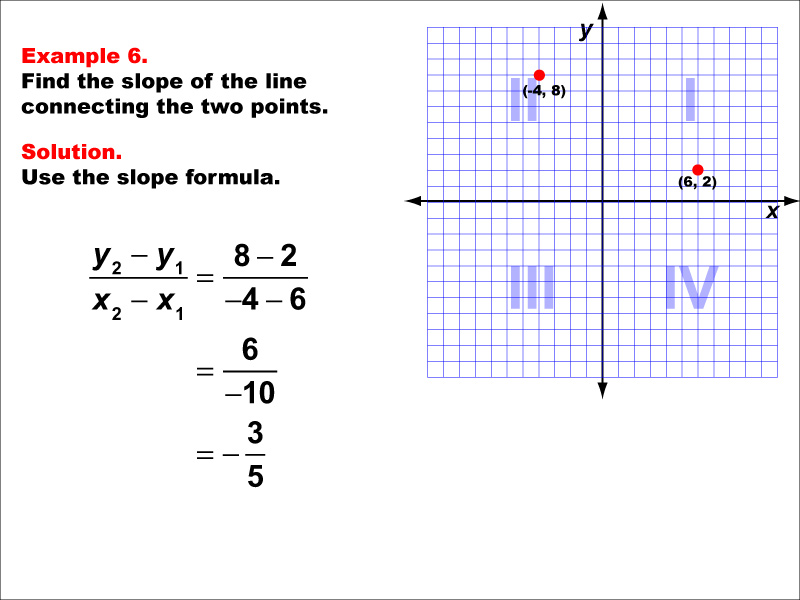
This example illustrates the calculation of slope for a line connecting two points in different quadrants: (-4, 8) in Quadrant II and (6, 2) in Quadrant I. Applying the slope formula, we find that the slope is (8 - 2) / (-4 - 6) = 6 / -10 = -3 / 5.
The slope formula is a fundamental concept in coordinate geometry, helping us understand the steepness and direction of lines. This example demonstrates how to handle points in different quadrants and interpret a negative slope.
Providing multiple examples like this allows students to encounter various scenarios, including those involving different quadrants and negative slopes. This helps reinforce the concept and improves their ability to calculate and interpret slopes in more complex situations.
Teacher's Script: Take a close look at this example. Notice that the slope is negative, indicating that the line is decreasing as we move from left to right. Remember, when we have a negative slope, it means that for every unit we move to the right, the line falls by the absolute value of the slope. In this case, for every 5 units we move horizontally to the right, the line falls by 3 units.
For a complete collection of math examples related to Slope Formula click on this link: Math Examples: Slope Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.5, CCSS.MATH.CONTENT.7.RP.A.2.D |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Slope |
| Copyright Year | 2013 |
| Keywords | slope, rise over run, slope formula |