Display Title
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 28
Display Title
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 28
Topic
Exponential Functions
Description
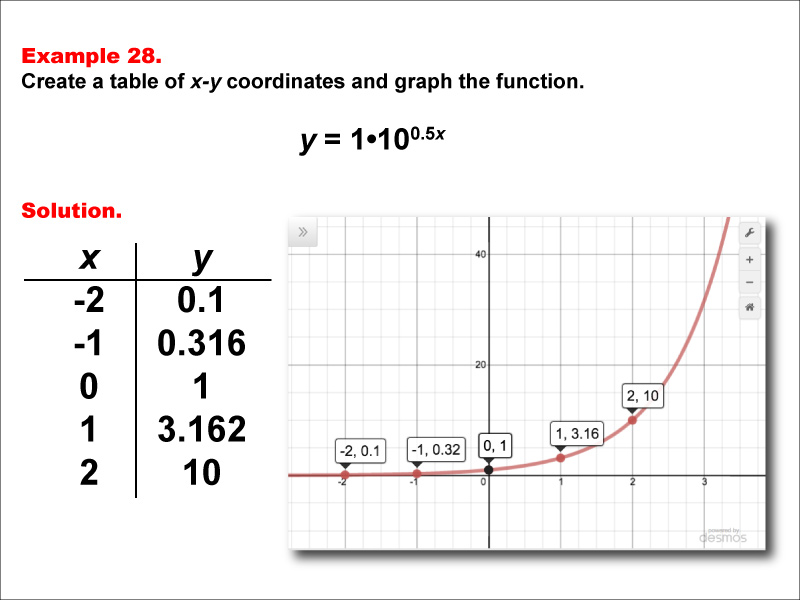
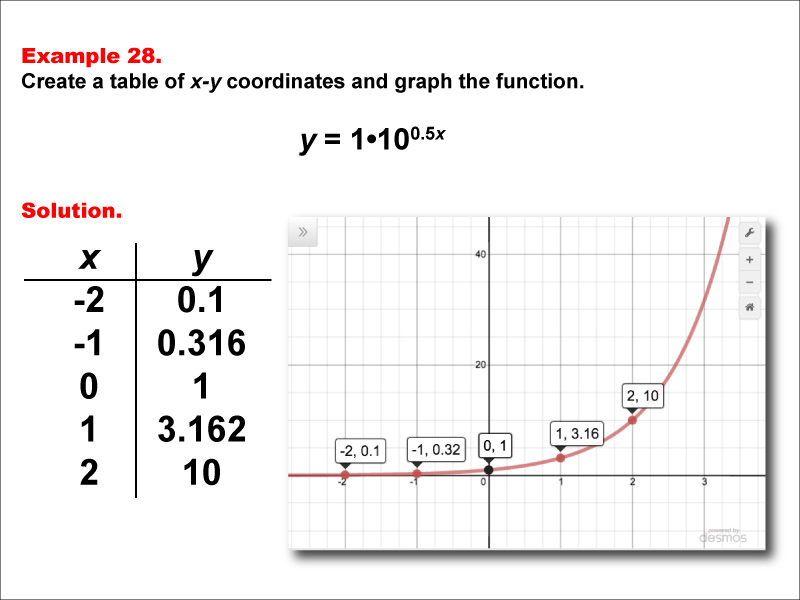
This math example demonstrates the creation of a table of x-y coordinates and the graphing of the exponential function y = 1 * 100.5x. The image showcases both a graph and a corresponding table, highlighting the behavior of this exponential function with a fractional exponent. The table includes key points such as (-2, 0.1), (-1, 0.316), (0, 1), (1, 3.162), and (2, 10), illustrating how the y-values increase at a slower rate compared to a standard exponential function.
Exponential functions are a fundamental concept in mathematics, with applications in various fields such as finance, biology, and physics. This collection of examples aids in teaching the topic by providing visual and numerical representations of different exponential functions, including those with fractional exponents. Students can observe how these factors affect the graph's shape, the rate of growth, and the overall behavior of the function, developing a more nuanced understanding of exponential relationships.
Presenting multiple worked-out examples is crucial for students to fully comprehend exponential functions. By examining diverse cases, students can identify patterns, compare different functions, and gain a deeper insight into the behavior of exponential relationships. This approach helps reinforce key concepts and enhances students' ability to analyze and interpret exponential functions in various real-world scenarios, such as population growth models, compound interest calculations, or radioactive decay processes.
Teacher Script: "Now, let's look at this exponential function, y = 1 * 100.5x. How does it compare to our previous examples? Notice the fractional exponent 0.5x. How does this affect the rate at which the function grows? Can you describe what happens to the y-values as x increases? This function demonstrates a slower exponential growth compared to y = 10x. How might we use this type of function to model real-world situations, such as the growth of a population with limited resources?"
For a complete collection of math examples related to Exponential Functions click on this link: Math Examples: Exponential Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7.E, CCSS.Math.CONTENT.HSF.LE.A.2, CCSS.MATH.CONTENT.HSF.LE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Exponential and Logarithmic Functions • Graphs of Exponential and Logarithmic Functions |
| Copyright Year | 2015 |
| Keywords | function, graphs of exponential functions, exponential function tables |