Display Title
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 34
Display Title
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 34
Topic
Exponential Functions
Description
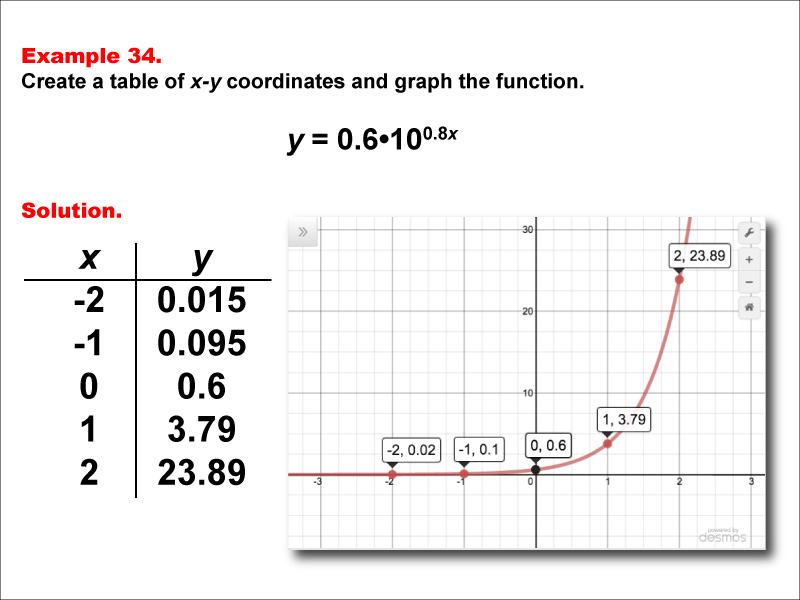
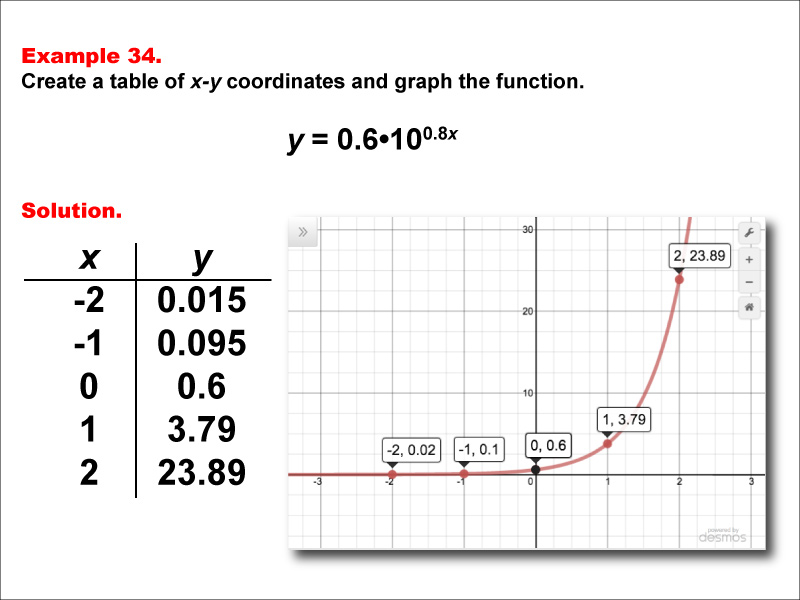
This math example presents the exponential function y = 0.6 * 100.8x through both a table of x-y coordinates and a graph. The table provides values for x ranging from -2 to 2, demonstrating how the function's output changes as x increases. The accompanying graph offers a visual representation of this exponential growth function, highlighting its distinctive shape and behavior.
Exponential functions are fundamental in mathematics and have numerous real-world applications, including modeling population growth, compound interest, and radioactive decay. This collection of examples aids in teaching the topic by offering students diverse representations of exponential functions, enabling them to observe how different parameters influence the function's behavior. By examining both tabular and graphical forms, students can develop a deeper understanding of the relationship between input and output values in exponential functions.
The importance of multiple worked-out examples in understanding exponential functions cannot be overstated. Each example in this set showcases a unique form of the exponential function, helping students identify patterns and comprehend how alterations in the base, coefficient, or exponent affect the function's graph and values. This variety of examples strengthens the concept and assists students in developing a more intuitive grasp of exponential behavior, preparing them to tackle more complex problems and real-world scenarios.
Teacher Script: "Now, let's analyze the function y = 0.6 * 100.8x. Notice how the y-values increase rapidly as x becomes positive, but at a different rate compared to our previous examples. The coefficient of 0.6 affects the y-intercept, while the exponent 0.8x influences the rate of growth. How does this graph compare to the ones we've seen before? Can you explain why it looks slightly different?"
For a complete collection of math examples related to Exponential Functions click on this link: Math Examples: Exponential Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7.E, CCSS.Math.CONTENT.HSF.LE.A.2, CCSS.MATH.CONTENT.HSF.LE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Exponential and Logarithmic Functions • Graphs of Exponential and Logarithmic Functions |
| Copyright Year | 2015 |
| Keywords | function, graphs of exponential functions, exponential function tables |