Display Title
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 44
Display Title
Math Example--Exponential Concepts--Exponential Functions in Tabular and Graph Form: Example 44
Topic
Exponential Functions
Description
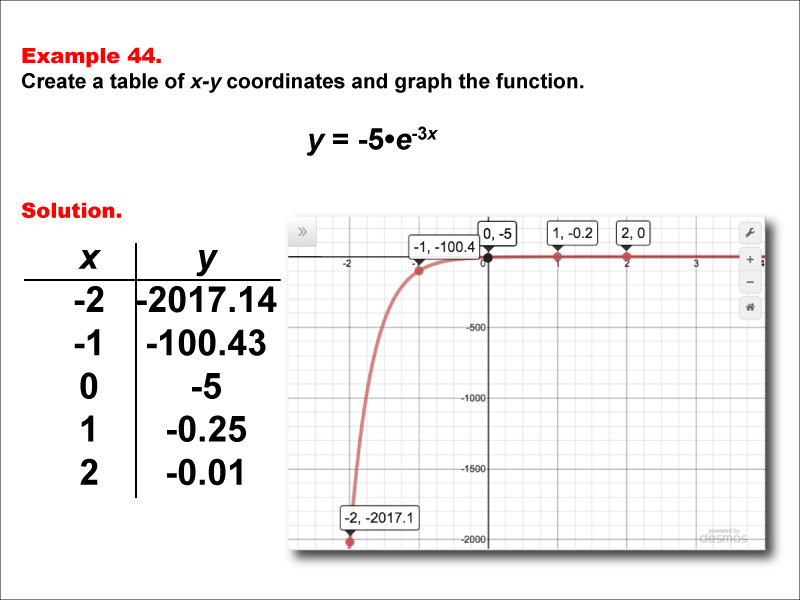
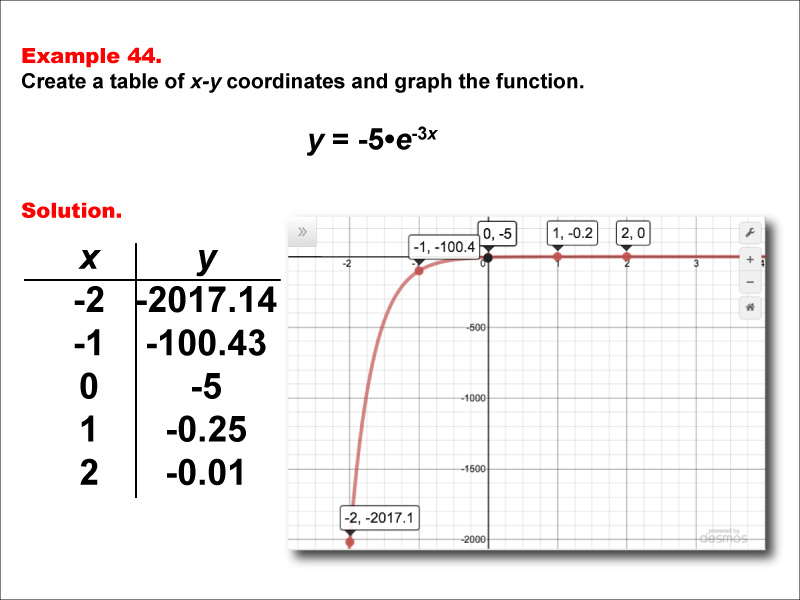
This math example illustrates the exponential function y = -5 * e-3x through both a table of values and a graph. The table presents x-y coordinates for x values from -2 to 2, demonstrating the extremely rapid change in the function's output as x increases. The accompanying graph provides a visual representation of this exponential growth function with a negative coefficient and tripled exponent, highlighting its steep curve and unique behavior.
Exponential functions with coefficients and modified exponents are fundamental in mathematics and have numerous real-world applications, such as modeling population dynamics, chemical reactions, and certain financial scenarios. This collection of examples aids in teaching the topic by offering students diverse representations of exponential functions, enabling them to observe how different parameters influence the function's behavior, particularly when dealing with negative coefficients and exponents containing factors.
The importance of multiple worked-out examples in understanding complex exponential functions cannot be overstated. Each example in this set showcases a unique form of the exponential function, helping students identify patterns and comprehend how alterations in the coefficient and exponent affect the function's graph and values. This variety of examples strengthens the concept and assists students in developing a more intuitive grasp of exponential behavior, especially in cases where the function exhibits extremely rapid growth or decay in the negative direction.
Teacher Script: "Let's examine the function y = -5 * e-3x. Notice the extremely rapid change in y-values as x varies. The negative coefficient of -5 not only flips the graph vertically but also stretches it, while the factor of 3 in the exponent dramatically increases the growth rate compared to a standard exponential function. Compare this graph to our previous examples. How does the combination of a negative coefficient and a tripled exponent affect the steepness and orientation of the curve? Can you think of any real-world scenarios where we might encounter such an extremely rapid exponential change in the negative direction?"
For a complete collection of math examples related to Exponential Functions click on this link: Math Examples: Exponential Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7.E, CCSS.Math.CONTENT.HSF.LE.A.2, CCSS.MATH.CONTENT.HSF.LE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Exponential and Logarithmic Functions • Graphs of Exponential and Logarithmic Functions |
| Copyright Year | 2015 |
| Keywords | function, graphs of exponential functions, exponential function tables |