Display Title
Math Example--Function Concepts--Building Functions: Example 10
Display Title
Math Example--Function Concepts--Building Functions: Example 10

Topic
Arithmetic
Description
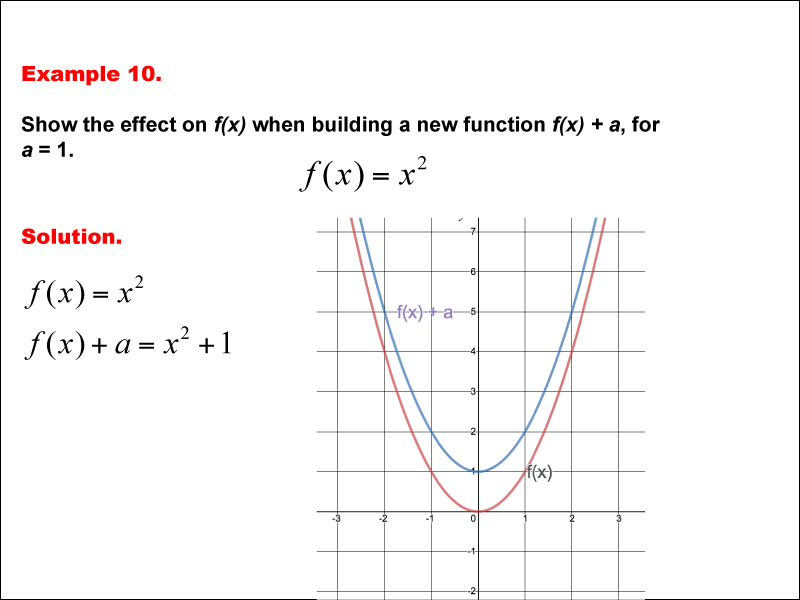
Analyze the effect of building a new function f(x) + a from f(x) = x2, where a = 1. Graph the transformation and calculate the new function. This example shows the effect on the function when the function f(x) = x2 shifts vertically by adding a to the output. substituting a = 1, the new function becomes f(x) + a = x2 + 1. the graph shifts one unit upward.
The topic of functions is fundamental in mathematics. By observing how different transformations—shifts, reflections, and scalings—impact the function, students can better understand the concept of functional relationships. These examples provide a hands-on approach to dissecting how functions behave under various operations, making abstract concepts tangible.
Seeing multiple worked-out examples helps students grasp concepts deeply. It allows them to recognize patterns, test their hypotheses, and correct misconceptions, building a strong foundation in function operations.
Teacher’s Script: Look at the function presented here, where the function f(x) = x2 shifts vertically by adding a to the output. substituting a = 1, the new function becomes f(x) + a = x2 + 1. the graph shifts one unit upward. Can you observe how the transformation changes the graph? Notice how this operation directly affects the function's behavior. Try applying a similar transformation to a different function to see if the pattern holds.
For a complete collection of math examples related to Functions click on this link: Math Examples: Building Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.BF.B.3 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2020 |
| Keywords | building functions |