Display Title
Math Example--Function Concepts--Building Functions: Example 11
Display Title
Math Example--Function Concepts--Building Functions: Example 11
Topic
Arithmetic
Description
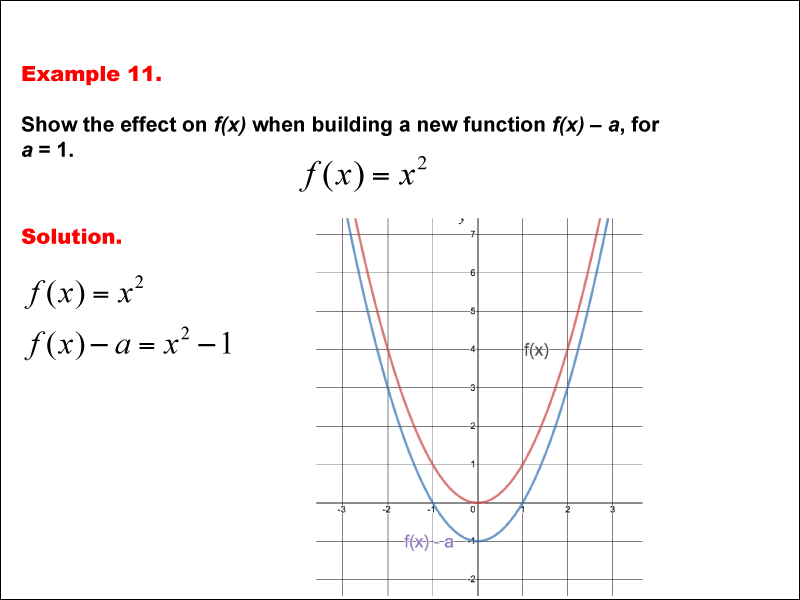
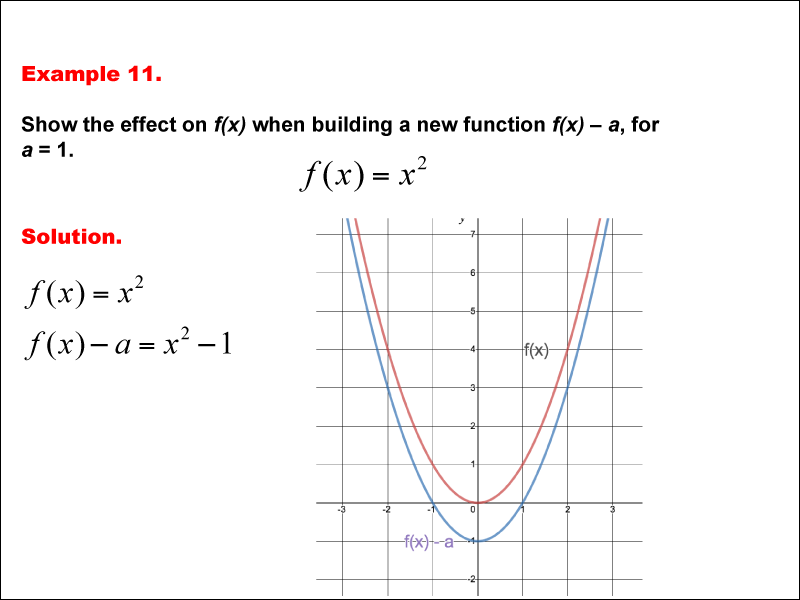
The problem involves analyzing the effect on the function f(x) = x2 when a constant a is subtracted. The specific scenario is for a = 1. The goal is to determine how the graph of f(x) is transformed. This example shows the effect on the function when subtracting a constant a from f(x) shifts the graph of f(x) downward by a units. for a = 1, the function becomes f(x) - a = x2 - 1. this results in a vertical shift down, as shown by the new graph in blue compared to the original in red.
The topic of functions is fundamental in mathematics. By observing how different transformations—shifts, reflections, and scalings—impact the function, students can better understand the concept of functional relationships. These examples provide a hands-on approach to dissecting how functions behave under various operations, making abstract concepts tangible.
Seeing multiple worked-out examples helps students grasp concepts deeply. It allows them to recognize patterns, test their hypotheses, and correct misconceptions, building a strong foundation in function operations.
Teacher’s Script: Look at the function presented here, where subtracting a constant a from f(x) shifts the graph of f(x) downward by a units. for a = 1, the function becomes f(x) - a = x2 - 1. this results in a vertical shift down, as shown by the new graph in blue compared to the original in red. Can you observe how the transformation changes the graph? Notice how this operation directly affects the function's behavior. Try applying a similar transformation to a different function to see if the pattern holds.
For a complete collection of math examples related to Functions click on this link: Math Examples: Building Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.BF.B.3 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2020 |
| Keywords | building functions |