Display Title
Math Example--Function Concepts--Domain and Range of a Function--Example 8
Display Title
Math Example--Function Concepts--Domain and Range of a Function--Example 8
Topic
Arithmetic
Description
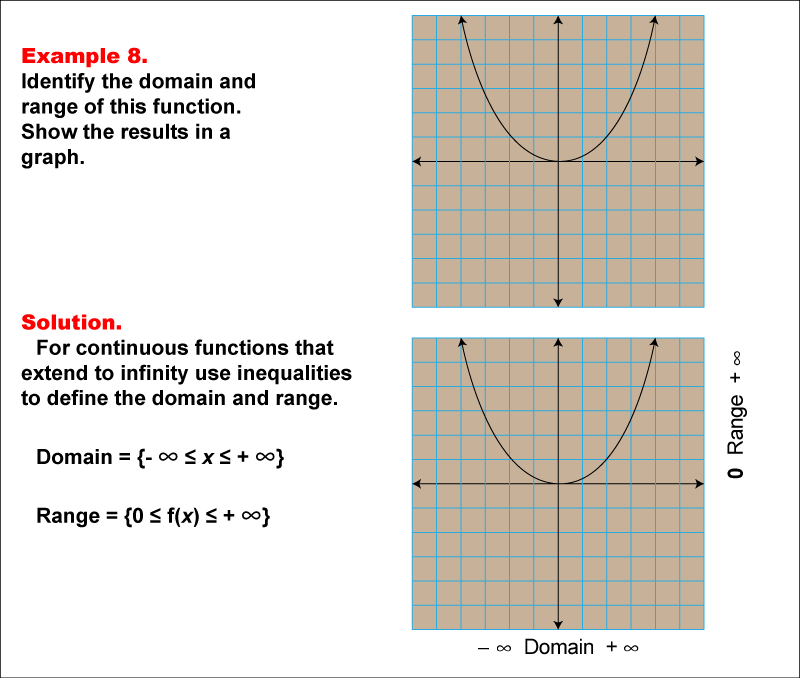
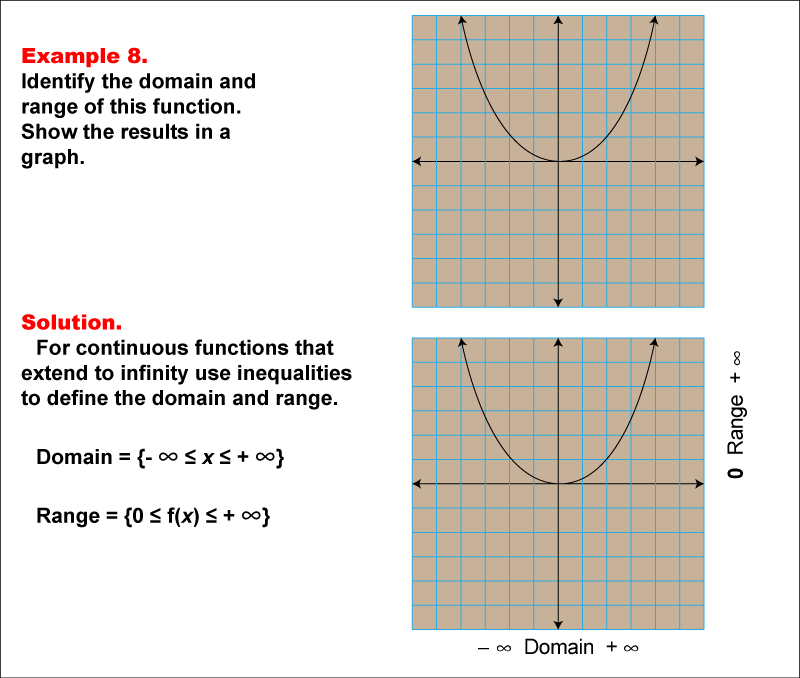
The example demonstrates identify the domain and range of a parabolic function with an infinite domain and range that starts from 0 and goes to positive infinity. graph the function and use inequalities to define the domain and range. This is illustrated by the accompanying image, which shows the function is a parabola opening upwards, indicating an unrestricted x-value range but a y-value range that is bounded below. the domain is -∞ ≤ x ≤ +∞, and the range is -∞ ≤ f(x) ≤ +∞. this solution highlights the parabolic shape, with the graph covering all x-values and a range restricted to non-negative values starting from the minimum value at the vertex of the parabola.
Functions are a fundamental concept in mathematics, providing students with an understanding of how different mathematical relationships can be analyzed and represented. By exploring these examples, students gain hands-on experience in identifying key attributes of functions.
Seeing multiple worked-out examples helps students understand patterns and variations in problem-solving. This scaffolds their learning and builds confidence in handling complex scenarios.
Teacher’s Script: In this example, notice how we analyze the relationship between the input values and their corresponding outputs. Observe how the graph helps to visually identify the domain and range. Use the image to determine the specific attributes discussed.
For a complete collection of math examples related to Functions click on this link: Math Examples: Domain and Range Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.8, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.A.1.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2020 |
| Keywords | functions |