Display Title
Math Example--Function Concepts--Functions and Their Inverses: Example 17
Display Title
Math Example--Function Concepts--Functions and Their Inverses: Example 17
Topic
Functions
Description
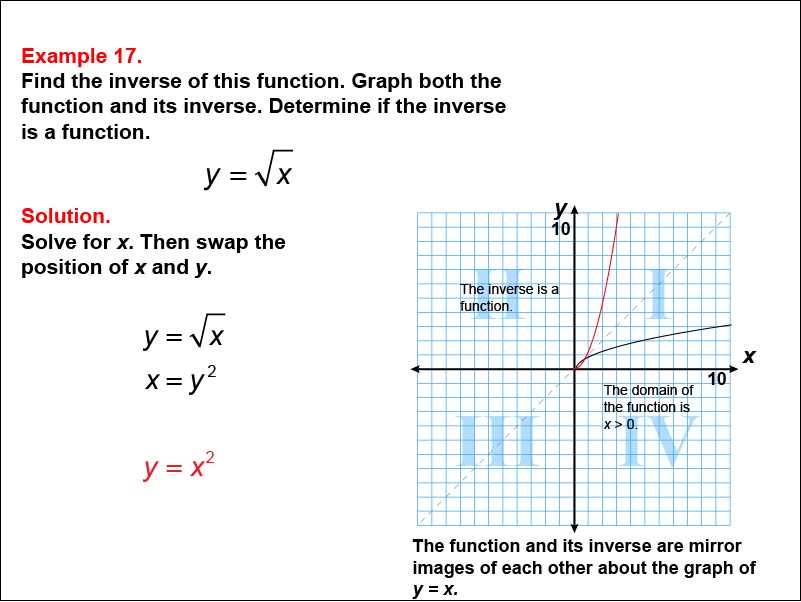
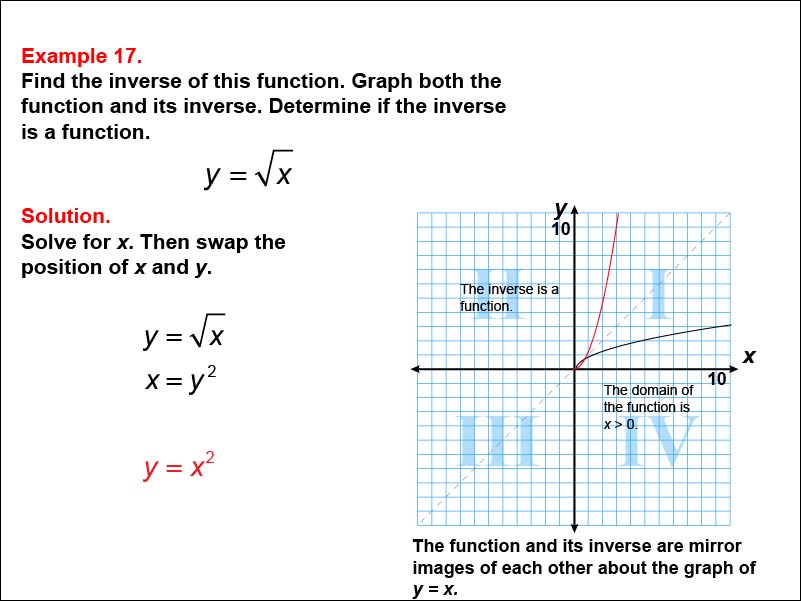
This example focuses on the square root function y = √x and its inverse. The graph shows both the original function and its inverse, y = x2, as mirror images about the line y = x, with the domain of the original function restricted to x ≥ 0. Students are challenged to find the inverse function by solving for x and then swapping x and y.
Understanding inverse functions is crucial in mathematics, particularly when working with root functions and their powers. This collection of examples offers a comprehensive look at various types of functions and their inverses, helping students understand the concept from multiple perspectives.
Exposure to multiple worked-out examples is essential for students to fully grasp the concept of inverse functions. Each example presents a unique scenario or function type, allowing students to recognize patterns and develop problem-solving strategies that can be applied to a wide range of mathematical situations.
In this example, focus on how we find the inverse of y = √x. The result is y = x2, with the domain of the original function restricted to ensure the inverse is also a function. Notice how the domain restriction on the original function allows both the function and its inverse to pass the vertical line test. Understanding this process will help you solve similar problems involving square roots and quadratic functions, and recognize the importance of domain restrictions in creating one-to-one functions.
For a complete collection of math examples related to Inverse Functions click on this link: Math Examples: Inverse Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.BF.B.4, CCSS.MATH.CONTENT.HSF.BF.B.4.A, CCSS.MATH.CONTENT.HSF.BF.B.4.B, CCSS.MATH.CONTENT.HSF.BF.B.4.C, CCSS.MATH.CONTENT.HSF.BF.B.4.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Functions and Their Inverses |
| Copyright Year | 2013 |
| Keywords | functions, inverses |