Display Title
Math Example--Function Concepts--Functions and Their Inverses: Example 18
Display Title
Math Example--Function Concepts--Functions and Their Inverses: Example 18
Topic
Functions
Description
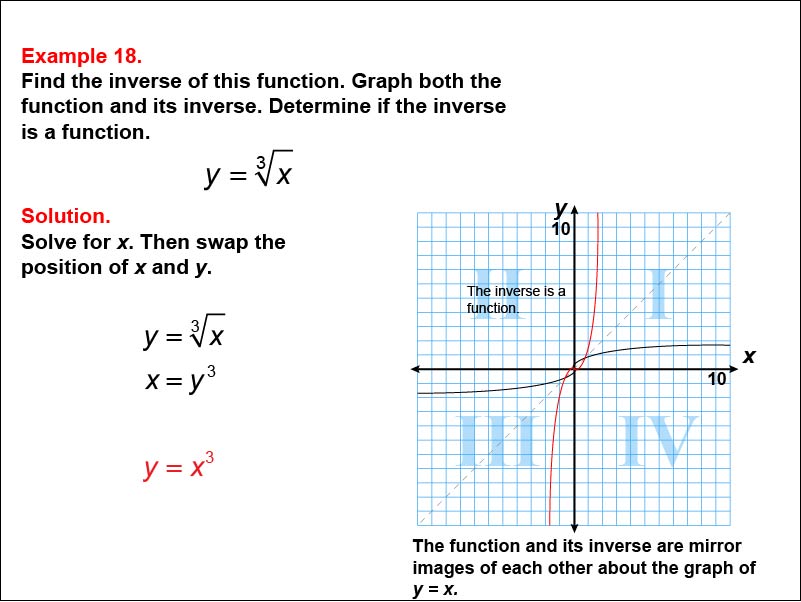
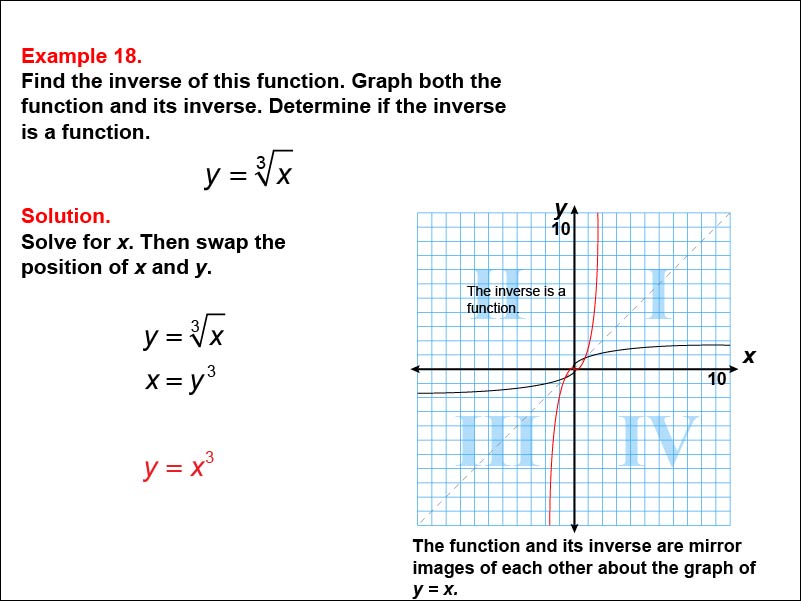
This example examines the cube root function y = ∛x and its inverse. The graph illustrates both the original function and its inverse, y = x3, as mirror images about the line y = x. Students are tasked with determining the inverse function by solving for x and then swapping x and y.
Understanding inverse functions is essential in mathematics, especially when dealing with root functions and their powers. This collection of examples provides a comprehensive look at various types of functions and their inverses, helping students grasp the concept from different angles.
Seeing multiple worked-out examples is crucial for students to fully understand the concept of inverse functions. Each example presents a unique scenario or function type, enabling students to recognize patterns and develop problem-solving strategies applicable to a wide range of mathematical situations.
For this example, pay attention to how we find the inverse of y = ∛x. The result is y = x3. Observe that both the original function and its inverse are indeed functions, as they pass the vertical line test. Unlike the square root function, the cube root function does not require domain restrictions to ensure its inverse is a function. Understanding this process will help you solve similar problems involving cube roots and cubic functions, and recognize the differences between even and odd root functions in terms of their inverses.
For a complete collection of math examples related to Inverse Functions click on this link: Math Examples: Inverse Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.BF.B.4, CCSS.MATH.CONTENT.HSF.BF.B.4.A, CCSS.MATH.CONTENT.HSF.BF.B.4.B, CCSS.MATH.CONTENT.HSF.BF.B.4.C, CCSS.MATH.CONTENT.HSF.BF.B.4.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Functions and Their Inverses |
| Copyright Year | 2013 |
| Keywords | functions, inverses |