Display Title
Math Example--Function Concepts--Functions and Their Inverses: Example 6
Display Title
Math Example--Function Concepts--Functions and Their Inverses: Example 6
Topic
Functions
Description
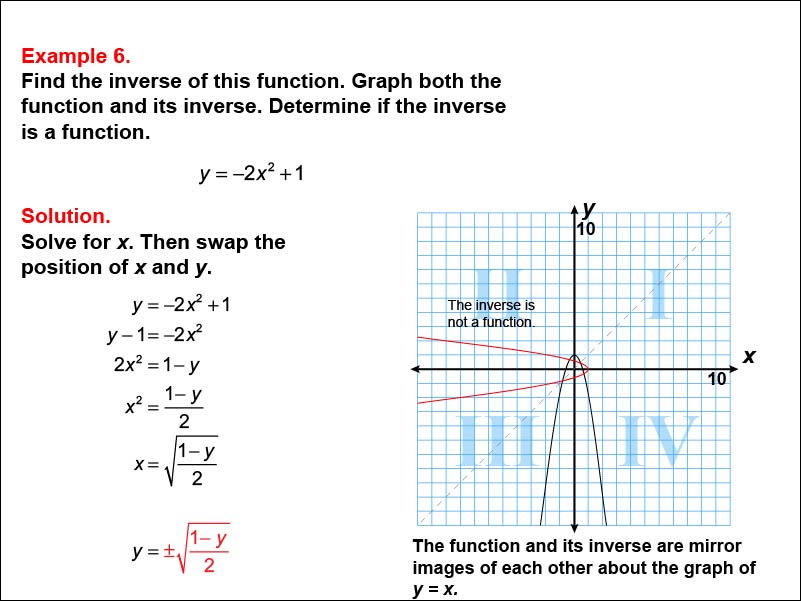
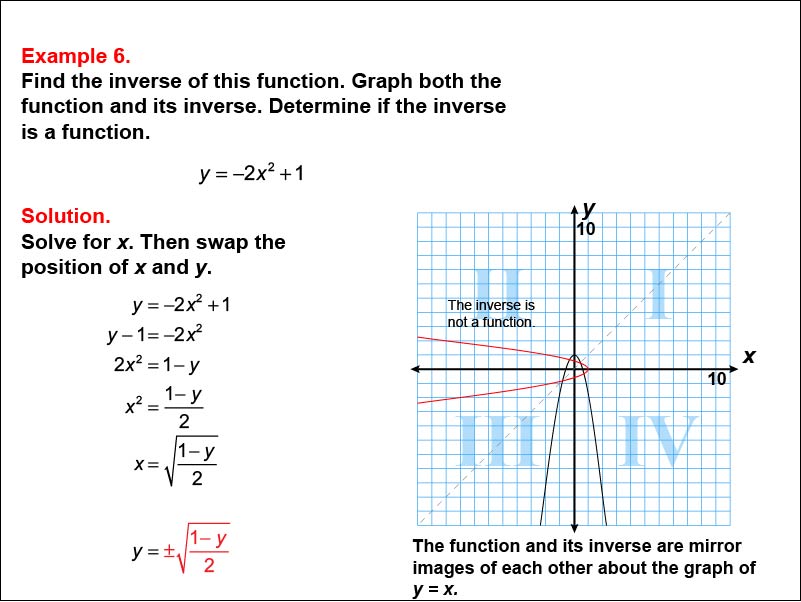
This example focuses on finding the inverse of the function y = -2x2 + 1. The graph shows a downward-opening parabola and its inverse, mirrored over the line y = x. Students are tasked with determining the inverse function, which involves solving for x, then swapping x and y.
Understanding inverse functions is crucial in mathematics as it allows students to explore the relationships between different functions and their inverses. This collection of examples provides a comprehensive look at various types of functions and their inverses, helping students grasp the concept from multiple angles.
Seeing multiple worked-out examples is essential for students to fully understand the concept of inverse functions. Each example presents a unique scenario or function type, allowing students to recognize patterns and develop problem-solving strategies that can be applied to a wide range of situations.
In this example, pay attention to how we find the inverse of the quadratic function y = -2x2 + 1. The result is y = ±√((1 - y) / 2). Notice that the inverse is not a function, as it fails the vertical line test. Understanding this process will help you solve similar problems effectively and recognize when an inverse is or is not a function.
For a complete collection of math examples related to Inverse Functions click on this link: Math Examples: Inverse Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.BF.B.4, CCSS.MATH.CONTENT.HSF.BF.B.4.A, CCSS.MATH.CONTENT.HSF.BF.B.4.B, CCSS.MATH.CONTENT.HSF.BF.B.4.C, CCSS.MATH.CONTENT.HSF.BF.B.4.D |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Functions and Their Inverses |
| Copyright Year | 2013 |
| Keywords | functions, inverses |