Display Title
Math Example--Function Concepts--Vertical Line Test--Example 1
Display Title
Math Example--Function Concepts--Vertical Line Test--Example 1
Topic
Arithmetic
Description
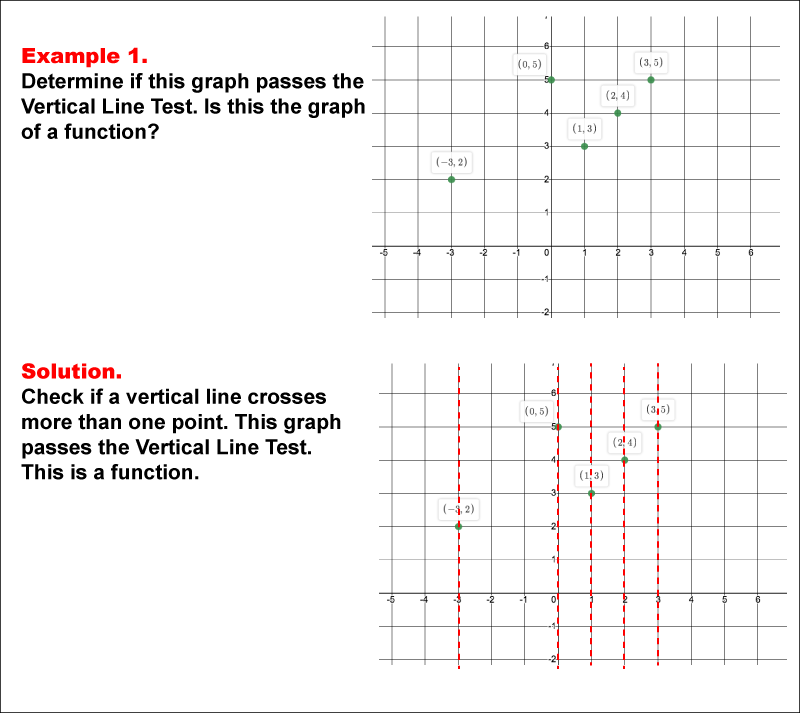
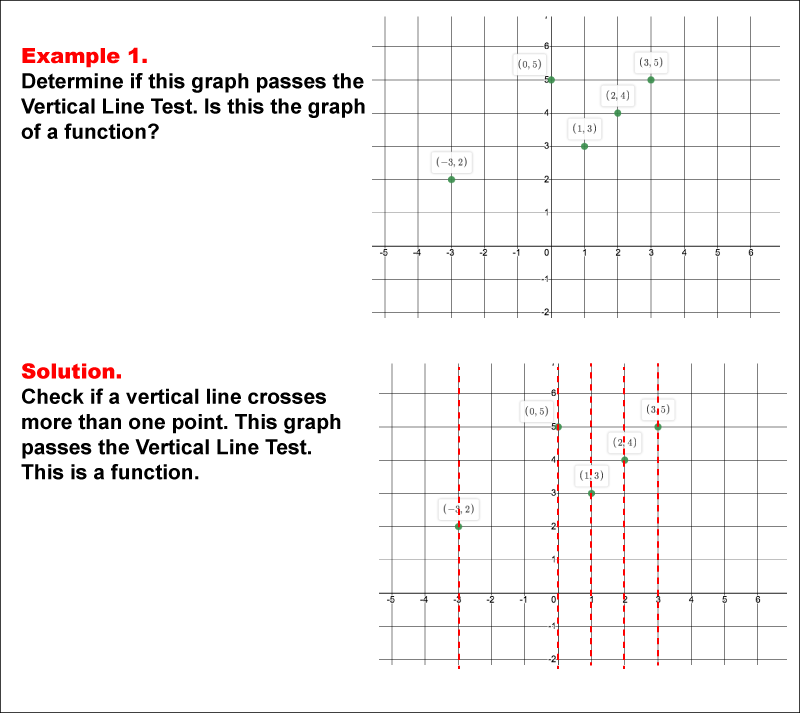
This example illustrates a scatter plot with several points labeled with their coordinates. The task is to determine whether the graph passes the vertical line test to qualify as a function. The solution demonstrates that no vertical line intersects the graph at more than one point, confirming that it is a function.
The Vertical Line Test is an essential concept in determining whether a graph represents a function. By drawing vertical lines across the graph, one can assess if any vertical line intersects the graph more than once, indicating it is not a function. The examples in this collection provide a visual and interactive way for students to comprehend this concept.
By observing multiple worked-out examples, students are better equipped to understand the nuances of a mathematical concept. These examples not only clarify the procedure but also reinforce understanding through varied applications.
Teacher’s Script: Let's examine this graph together. Notice how we apply the Vertical Line Test by imagining or drawing vertical lines through the graph. In this example, this image shows a scatter plot with several points labeled with their coordinates. the task is to determine whether the graph passes the vertical line test to qualify as a function. the solution demonstrates that no vertical line intersects the graph at more than one point, confirming that it is a function. What does this tell us about whether this is a function?
For a complete collection of math examples related to Functions click on this link: Math Examples: Vertical Line Test Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.8, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.A.1.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2020 |
| Keywords | functions |