edcom-728x90

IXL Ad

GraphingLogFunctions9.jpg
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Exponential and Logarithmic Functions >> Graphs of Exponential and Logarithmic Functions

Math Example: Graphs of Logarithmic Functions: Example 09

Math Example: Graphs of Logarithmic Functions: Example 09

Graph of y = -log_10(2x) + 4

Topic

Logarithmic Functions

Description

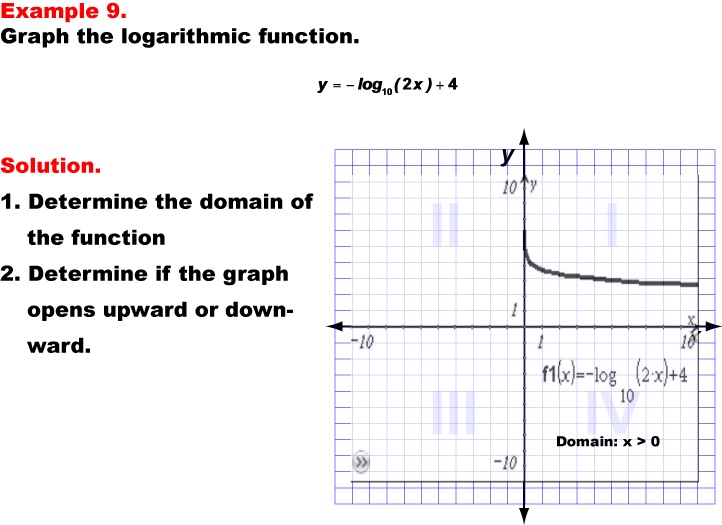
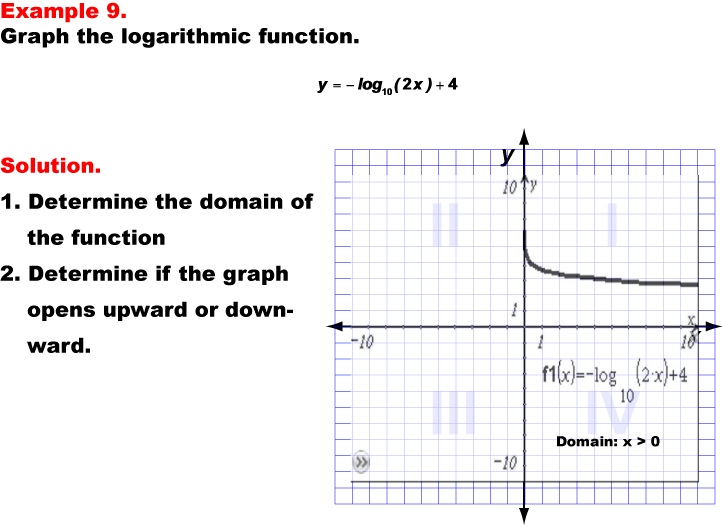
This example illustrates the graph of the logarithmic function y = -log10(2x) + 4. The graph opens downward due to the negative sign before the logarithm, demonstrating how the combination of a negative coefficient, multiplication inside the logarithm, and addition outside the logarithm affect the function's behavior. The domain of this function is x > 0, as the logarithm is only defined for positive values inside the parentheses.

Logarithmic functions play a crucial role in various mathematical and scientific applications, from modeling exponential growth and decay to solving complex equations. This collection of examples helps teach logarithmic functions by presenting a range of equations with different parameters and transformations, allowing students to visualize and understand how these changes impact the graph's shape, position, and properties.

Exploring multiple worked-out examples is vital for students to develop a comprehensive understanding of logarithmic functions. Each example builds upon previous knowledge, introducing new concepts and transformations. This approach helps students recognize patterns, make connections between different forms of logarithmic equations, and develop problem-solving skills that can be applied to more complex scenarios.

Teacher's Script: Let's examine our ninth example, y = -log10(2x) + 4. This graph introduces a new transformation - the negative sign before the logarithm. How does this change the overall shape of the graph compared to previous examples? Notice that the graph now opens downward. The multiplication by 2 inside the logarithm affects the horizontal position, while the addition of 4 shifts the graph vertically. Despite these changes, the domain remains x > 0. Can you identify where this graph intersects the y-axis? How does the negative sign affect the rate at which the function decreases?

For a complete collection of math examples related to Logarithmic Functions click on this link: Math Examples: Graphs of Logarithmic Functions Collection.

Common Core Standards CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.8.B, CCSS.MATH.CONTENT.HSF.BF.B.5, CCSS.MATH.CONTENT.HSF.IF.C.7.E, CCSS.Math.CONTENT.HSF.LE.A.2, CCSS.MATH.CONTENT.HSF.LE.A.3, CCSS.MATH.CONTENT.HSF.LE.A.4, CCSS.MATH.CONTENT.HSF.LE.B.5
Grade Range 9 - 12
Curriculum Nodes Algebra
    • Exponential and Logarithmic Functions
        • Graphs of Exponential and Logarithmic Functions
Copyright Year 2013
Keywords logarithmic functions, graphs