Display Title
Math Example: Graphs of Logarithmic Functions: Example 10
Display Title
Math Example: Graphs of Logarithmic Functions: Example 10
Topic
Logarithmic Functions
Description
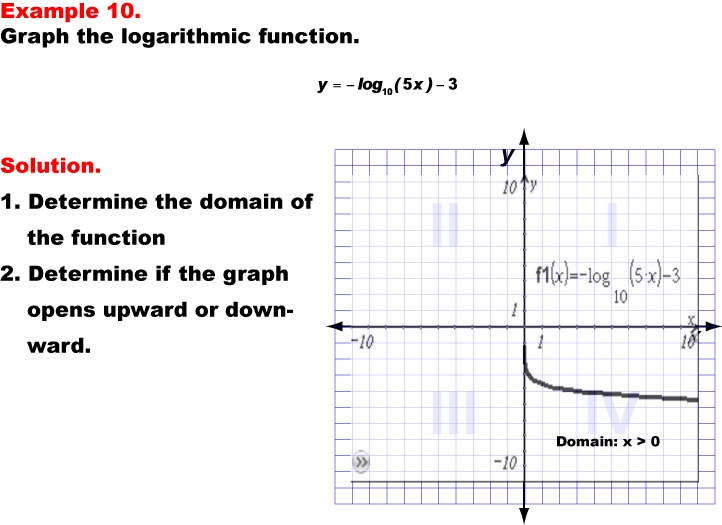
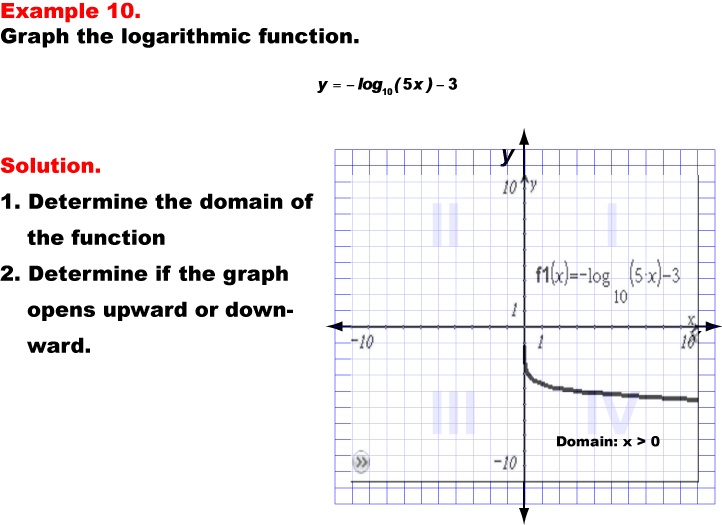
This example showcases the graph of the logarithmic function y = -log10(5x) - 3. The graph opens downward due to the negative sign before the logarithm, demonstrating how the combination of a negative coefficient, multiplication inside the logarithm, and subtraction outside the logarithm affect the function's behavior. The domain of this function is x > 0, as the logarithm is only defined for positive values inside the parentheses.
Logarithmic functions are essential in various fields, including science, engineering, and finance. They are particularly useful for modeling phenomena that exhibit exponential growth or decay. This collection of examples helps teach logarithmic functions by presenting a variety of equations with different transformations, allowing students to visualize and understand how these changes affect the graph's shape, position, and behavior.
Providing multiple worked-out examples is crucial for students to fully grasp the concept of logarithmic functions. Each example builds upon previous ones, introducing new transformations and combinations of operations. This approach helps students recognize patterns, understand the effects of different parameters, and develop the ability to predict how changes in the equation will impact the graph.
Teacher's Script: Now, let's examine our tenth example, y = -log10(5x) - 3. Compare this graph to the previous example. Both have a negative sign before the logarithm, so they open downward. How does the multiplication by 5 inside the logarithm affect the graph's horizontal position compared to the previous example? What about the subtraction of 3 outside the logarithm -- how does that change the graph's vertical position? Notice that despite these transformations, the domain remains x > 0. Can you predict where this graph will intersect the y-axis? How does the combination of these transformations affect the overall steepness of the graph?
For a complete collection of math examples related to Logarithmic Functions click on this link: Math Examples: Graphs of Logarithmic Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.8.B, CCSS.MATH.CONTENT.HSF.BF.B.5, CCSS.MATH.CONTENT.HSF.IF.C.7.E, CCSS.Math.CONTENT.HSF.LE.A.2, CCSS.MATH.CONTENT.HSF.LE.A.3, CCSS.MATH.CONTENT.HSF.LE.A.4, CCSS.MATH.CONTENT.HSF.LE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Exponential and Logarithmic Functions • Graphs of Exponential and Logarithmic Functions |
| Copyright Year | 2013 |
| Keywords | logarithmic functions, graphs |