Display Title
Math Example: Graphs of Logarithmic Functions: Example 28
Display Title
Math Example: Graphs of Logarithmic Functions: Example 28
Topic
Logarithmic Functions
Description
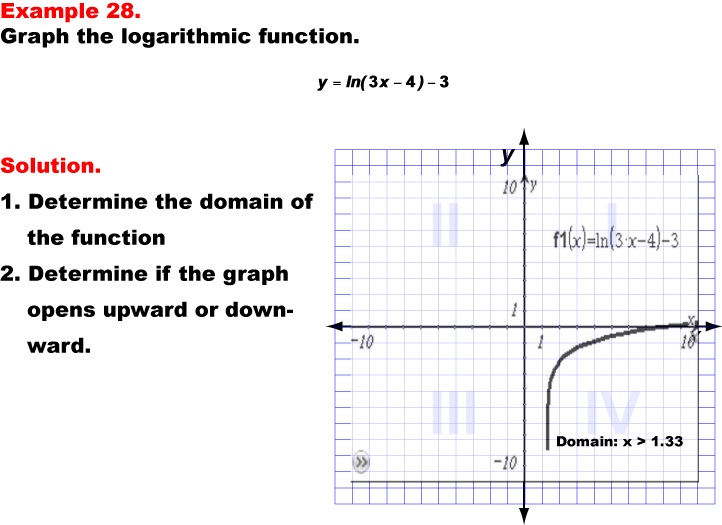
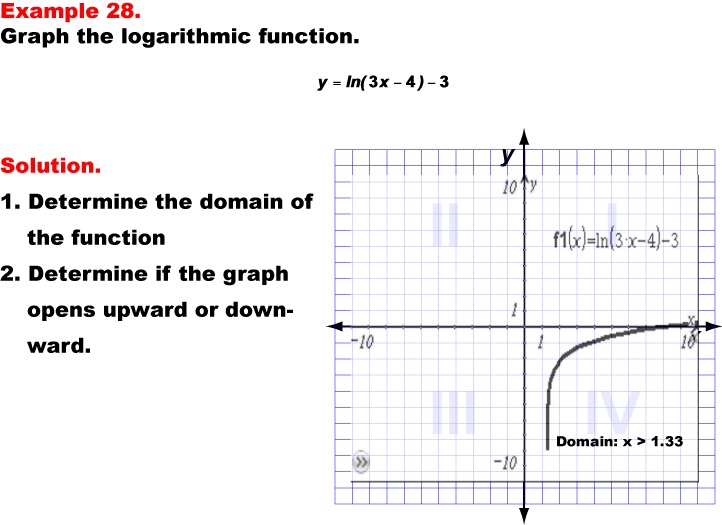
This example presents the graph of the natural logarithmic function y = ln(3x - 4) - 3. The graph opens upward, curving from left to right, demonstrating how the combination of multiplication and subtraction inside the logarithm, along with subtraction outside, affects the function's behavior. The domain of this function is x > 4/3, as the expression inside the natural logarithm must be positive.
Natural logarithmic functions with various transformations are essential in many scientific and mathematical applications, particularly in calculus and differential equations. They are often used to model complex growth and decay processes in fields such as biology, physics, and economics. This collection of examples helps teach logarithmic functions by presenting a range of equations with different parameters, allowing students to visualize and understand how these changes impact the graph's shape, position, domain, and range.
Providing multiple worked-out examples is crucial for students to fully grasp the concept of logarithmic functions and their transformations. Each example builds upon previous ones, introducing new variations and operations. This approach helps students recognize patterns, understand the effects of different parameters, and develop the ability to predict how changes in the equation will impact the graph of logarithmic functions.
Teacher's Script: Now, let's examine our final example, y = ln(3x - 4) - 3. Compare this graph to the previous natural logarithm function we just saw. What are the main differences you notice? The domain has changed to x > 4/3. Can you explain why? Consider how the expression 3x - 4 inside the logarithm affects where the graph intersects the x-axis. Then, think about how the subtraction of 3 outside the logarithm impacts the vertical position. Can you predict where this graph will intersect the y-axis? How do these transformations impact the overall behavior of the function compared to the previous example with addition inside and outside the logarithm?
For a complete collection of math examples related to Logarithmic Functions click on this link: Math Examples: Graphs of Logarithmic Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.8.B, CCSS.MATH.CONTENT.HSF.BF.B.5, CCSS.MATH.CONTENT.HSF.IF.C.7.E, CCSS.Math.CONTENT.HSF.LE.A.2, CCSS.MATH.CONTENT.HSF.LE.A.3, CCSS.MATH.CONTENT.HSF.LE.A.4, CCSS.MATH.CONTENT.HSF.LE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Exponential and Logarithmic Functions • Graphs of Exponential and Logarithmic Functions |
| Copyright Year | 2013 |
| Keywords | logarithmic functions, graphs |