Display Title
Math Example--Inequalities-- Linear Inequalities: Example 8
Display Title
Math Example--Inequalities-- Linear Inequalities: Example 8
Topic
Inequalities
Description
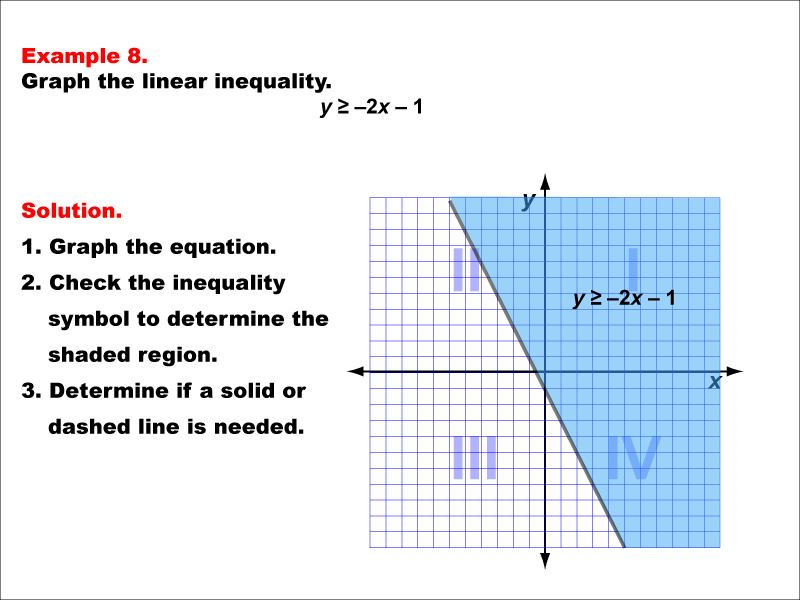
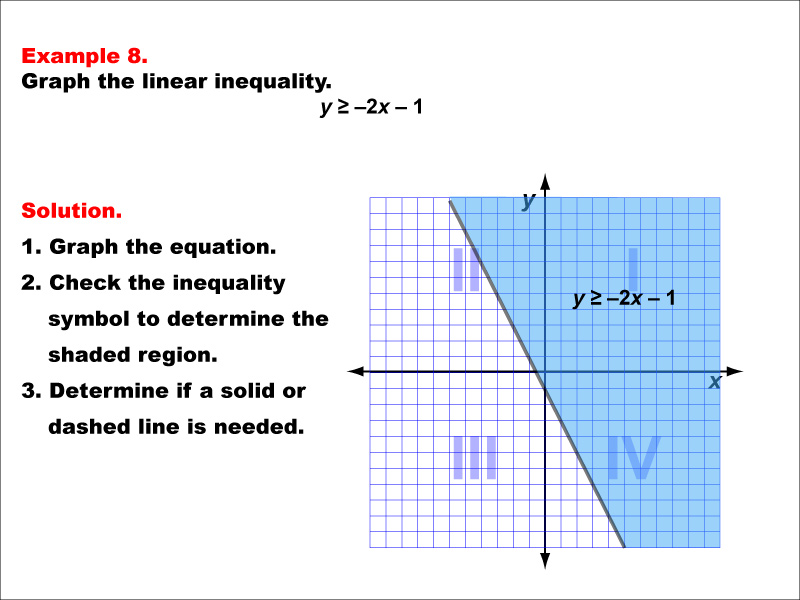
This example illustrates the graphing of the linear inequality y ≥ -2x - 1. The graph features a solid line representing the equation y = -2x - 1, with the area above the line shaded to indicate the region where the inequality is satisfied. Quadrants I and IV are predominantly shaded, demonstrating the solution set of this inequality. The solid line signifies that points on the line are included in the solution.
Linear inequalities are a fundamental concept in algebra, building upon students' understanding of linear equations and expanding it to include regions of the coordinate plane. This collection of examples aids in teaching this topic by providing visual representations of various inequalities, helping students grasp how different inequality symbols and equations translate into graphical form.
The importance of multiple worked-out examples cannot be overstated in helping students fully comprehend linear inequalities. Each example in this set highlights a different aspect of inequalities, allowing students to recognize patterns and develop a thorough understanding of how to graph and interpret these mathematical relationships.
Teacher's Script: Now, let's look at the inequality y ≥ -2x - 1. Notice how we first graph the line y = -2x - 1, then shade the region above it. The solid line shows that points on the line are part of our solution. Can you explain why Quadrants I and IV are mostly shaded in this example? How does this compare to the previous example with a similar inequality symbol?
For a complete collection of math examples related to Inequalities click on this link: Math Examples: Inequalities Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.EE.B.5, CCSS.MATH.CONTENT.7.EE.B.4.B, CCSS.MATH.CONTENT.HSA.REI.D.12 |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Inequalities |
| Copyright Year | 2013 |
| Keywords | linear equations, inequalities |