Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1
Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1
Topic
Linear Functions
Description
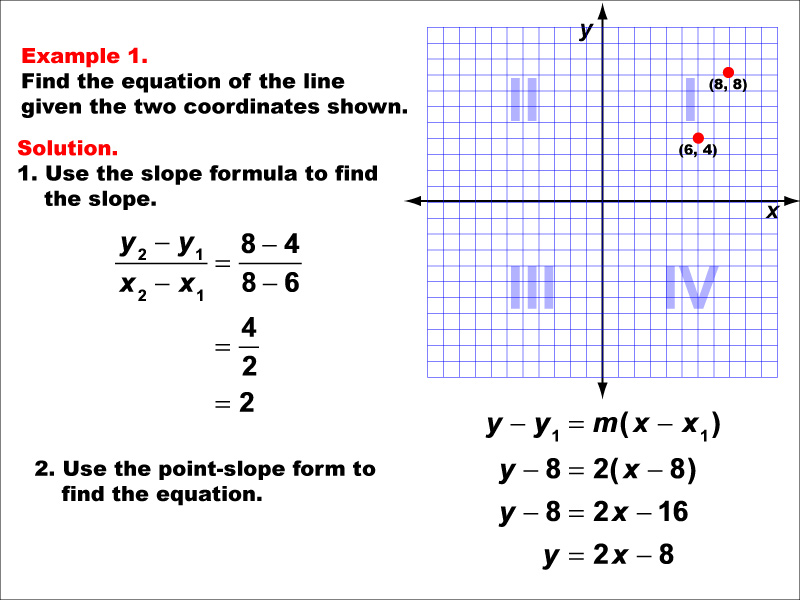
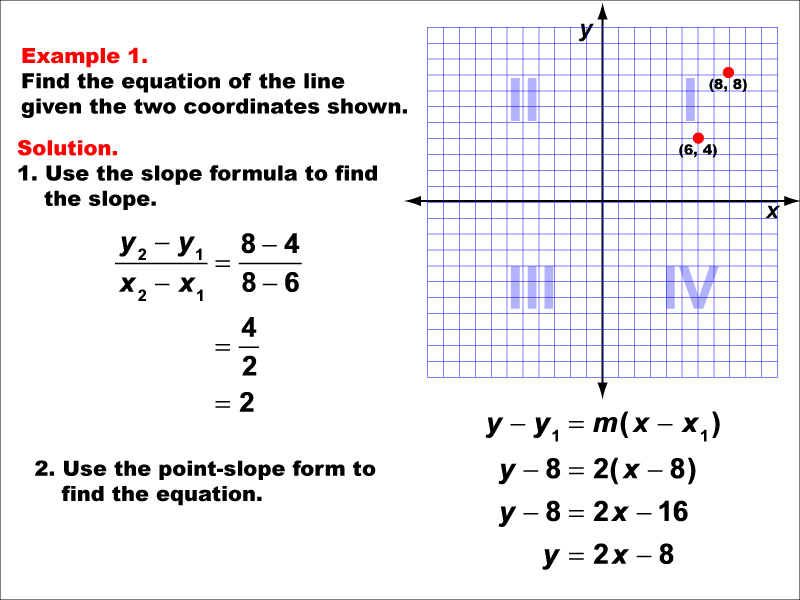
This example demonstrates how to find the equation of a line passing through two given points: (6, 4) and (8, 8). The slope is calculated using the formula (y2 - y1) / (x2 - x1), resulting in a slope of 2. Using the point-slope form of a line, y - y1 = m(x - x1), the equation is derived as y - 8 = 2(x - 8), which simplifies to y = 2x - 8.
Linear functions are fundamental in algebra and have numerous real-world applications. This collection of examples helps teach the concept by providing various scenarios, including positive and negative slopes, horizontal and vertical lines. By presenting different cases, students can develop a comprehensive understanding of how to determine the equation of a line given two points.
Exposure to multiple worked-out examples is crucial for students to fully grasp this concept. Each example reinforces the steps involved in finding the equation of a line, while also highlighting unique situations that may arise, such as horizontal or vertical lines. This repetition helps students recognize patterns and build confidence in their problem-solving abilities.
Teacher's Script: Now, let's look at our first example. We have two points on a line: (6, 4) and (8, 8). To find the equation of this line, we'll first calculate the slope using the slope formula. Then, we'll use the point-slope form to write our equation. Remember, practice makes perfect, so pay attention to the steps we're following here.
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.6, CCSS.MATH.CONTENT.8.EE.B.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Point-Slope Form • Slope-Intercept Form |
| Copyright Year | 2013 |
| Keywords | point-slope form, slope-intercept form, linear equations |