Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17
Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17
Topic
Linear Functions
Description
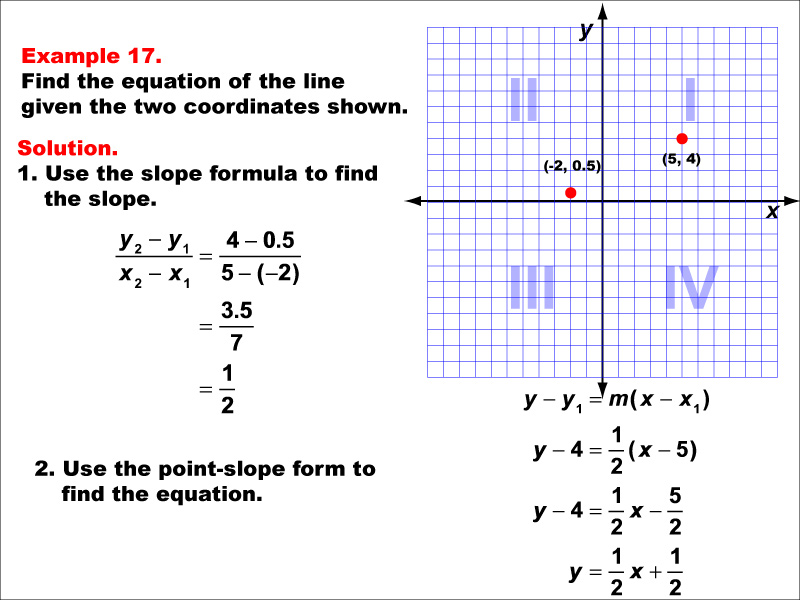
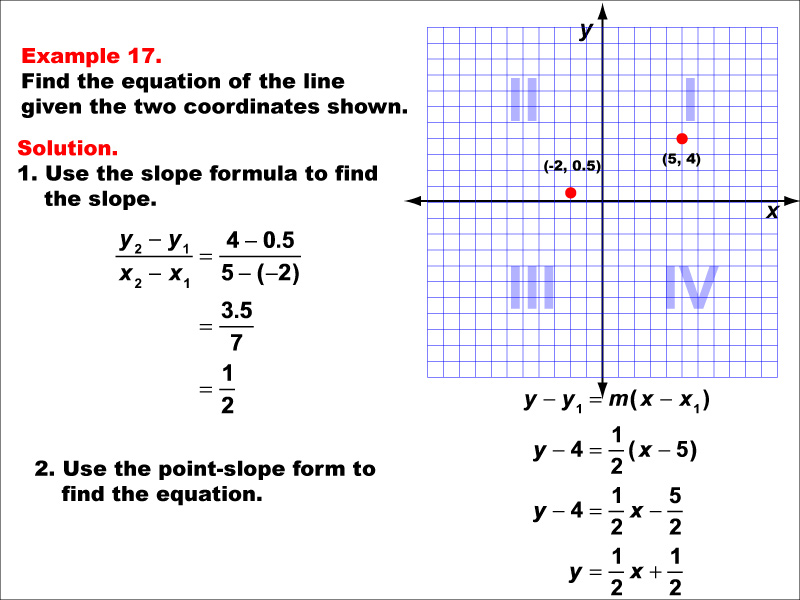
This image shows a graph with two points plotted at (-2, 0.5) and (5, 4). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (4 - 0.5) / (5 - (-2)) = 3.5 / 7 = 1 / 2. The point-slope form is used to find the equation: y - 4 = (1 / 2)(x - 5), resulting in y = (1 / 2)x + 1 / 2.
This example illustrates the process of finding a line equation when dealing with fractional coordinates and slopes. It reinforces the importance of precise calculations in mathematics and demonstrates how to simplify fractions in the final equation. Understanding how to work with fractions in linear functions is crucial for students as they progress to more complex mathematical concepts.
Exposure to various types of linear functions, including those with fractional components, is essential for building a strong foundation in algebra. This example helps students develop their skills in manipulating fractions and reinforces the connection between graphical representations and algebraic equations. Such practice is invaluable for developing mathematical fluency and problem-solving abilities.
Teacher's Script: In this example, we're working with fractional coordinates. Don't let that intimidate you! We'll use the same process as before, carefully calculating our slope and using the point-slope form. Notice how we end up with fractions in our final equation. This is perfectly okay and often more precise than decimal approximations. Remember, in mathematics, precision is key!
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.6, CCSS.MATH.CONTENT.8.EE.B.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Point-Slope Form • Slope-Intercept Form |
| Copyright Year | 2013 |
| Keywords | point-slope form, slope-intercept form, linear equations |