Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23
Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23
Topic
Linear Functions
Description
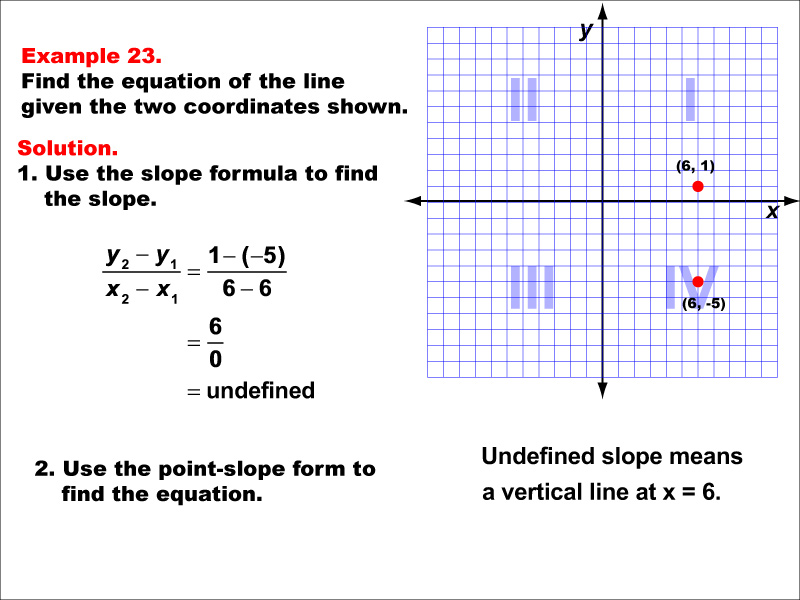
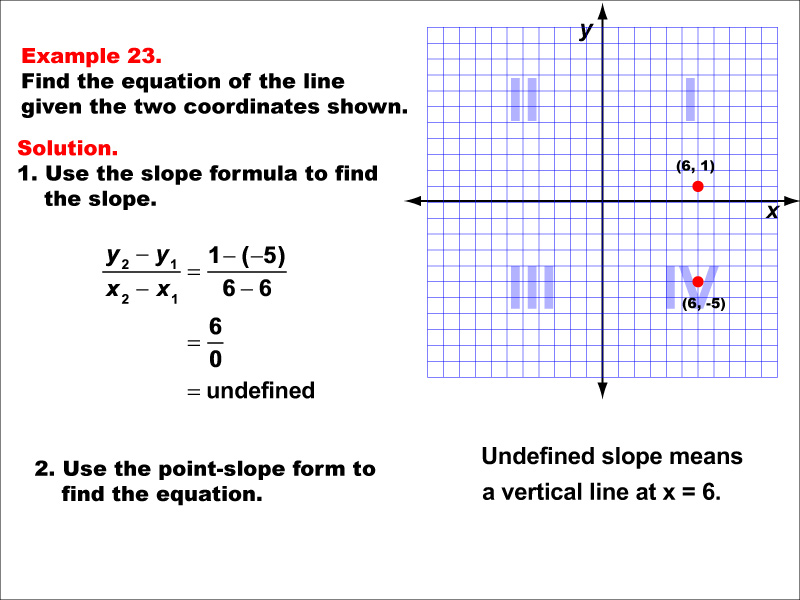
The image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6.
Vertical lines are a special case in linear functions, where the x-coordinate remains constant while the y-coordinate varies. This example helps students understand that not all linear relationships can be expressed in the standard slope-intercept form (y = mx + b). It demonstrates that when two points have the same x-coordinate, the result is a vertical line with an undefined slope.
Exposure to various types of linear functions, including vertical lines, is crucial for students to develop a comprehensive understanding of the concept. This example reinforces the idea that linear functions can take different forms and helps students recognize when standard formulas may not apply. Such knowledge is essential for problem-solving in more advanced mathematical concepts and real-world applications.
Teacher's Script: Now, let's look at a special case: a vertical line. Notice that both points have the same x-coordinate. What happens when we try to calculate the slope? That's right, we get division by zero, which is undefined. In this case, our line equation is simply x = 6. Remember, vertical lines are unique because they have an undefined slope and their equations are always in the form x = (constant).
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.6, CCSS.MATH.CONTENT.8.EE.B.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Point-Slope Form • Slope-Intercept Form |
| Copyright Year | 2013 |
| Keywords | point-slope form, slope-intercept form, linear equations |