Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28
Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28
Topic
Linear Functions
Description
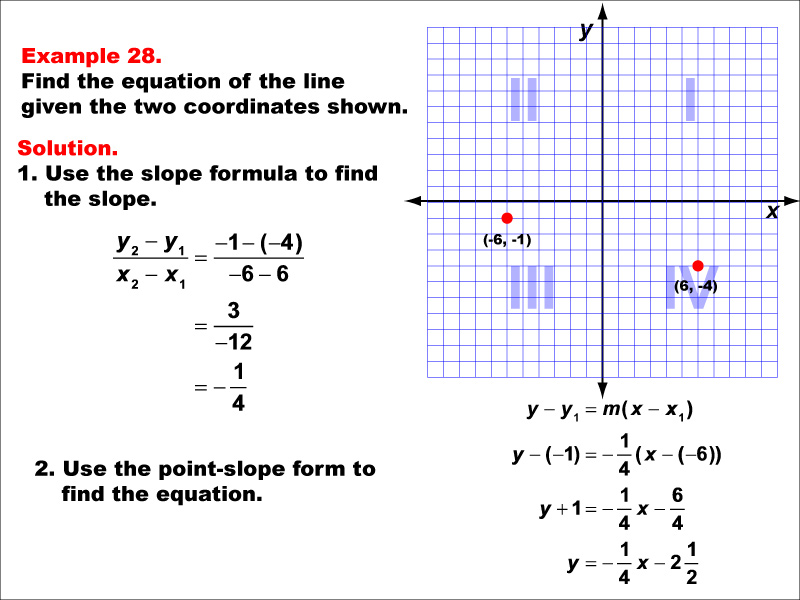
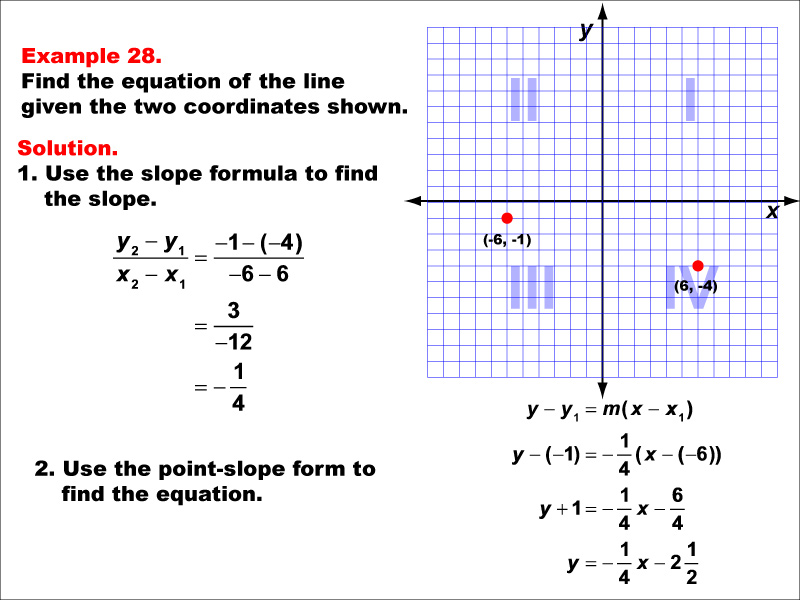
A graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2).
This example illustrates the process of finding a line equation when dealing with negative fractional slopes. It reinforces the importance of precise calculations in mathematics and demonstrates how to simplify fractions in the final equation. Understanding how to work with negative fractions in linear functions is crucial for students as they progress to more complex mathematical concepts.
Exposure to various types of linear functions, including those with negative fractional components, is essential for building a strong foundation in algebra. This example helps students develop their skills in manipulating fractions and reinforces the connection between graphical representations and algebraic equations. Such practice is invaluable for developing mathematical fluency and problem-solving abilities.
Teacher's Script: In this example, we're working with points that give us a negative fractional slope. Don't let that intimidate you! We'll use the same process as before, carefully calculating our slope and using the point-slope form. Notice how we end up with a negative fraction in our final equation. This is perfectly okay and often more precise than decimal approximations. Think about what this negative fractional slope means for the direction and steepness of our line.
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.6, CCSS.MATH.CONTENT.8.EE.B.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Point-Slope Form • Slope-Intercept Form |
| Copyright Year | 2013 |
| Keywords | point-slope form, slope-intercept form, linear equations |