Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29
Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29
Topic
Linear Functions
Description
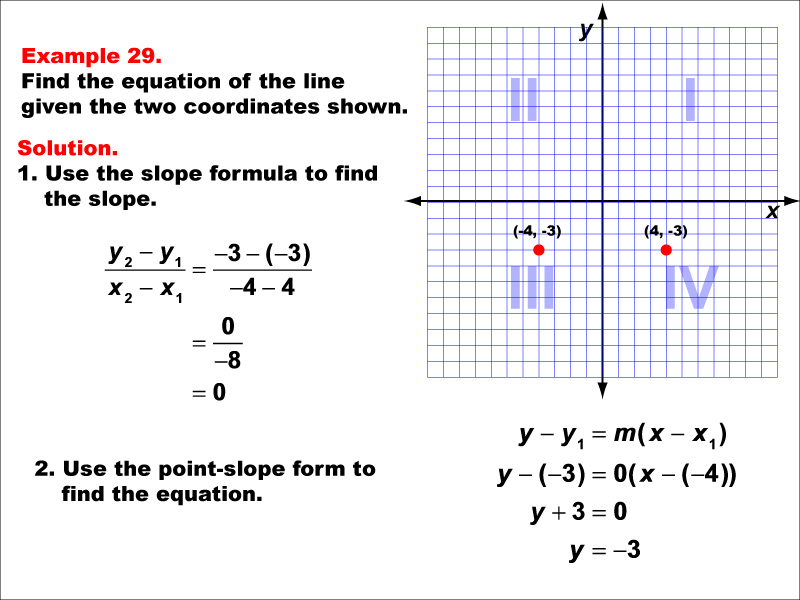
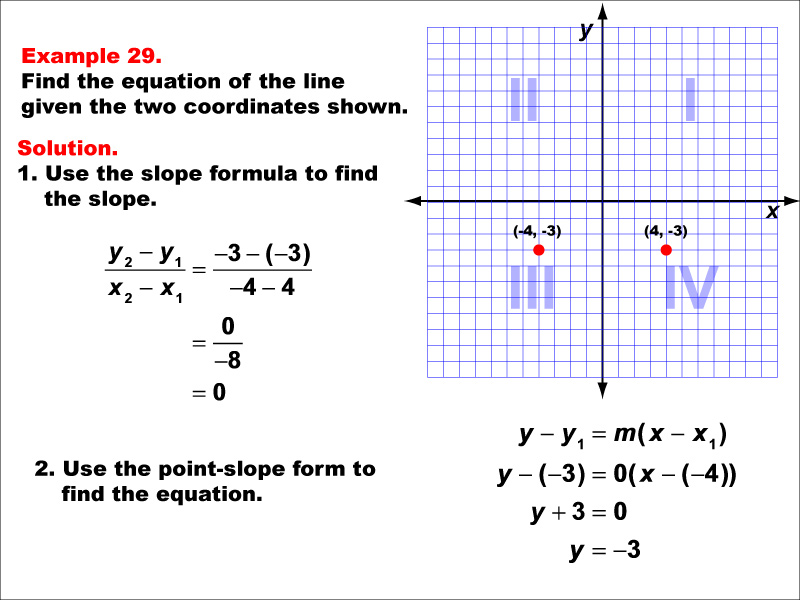
The image shows a worked-out example of finding the equation of a line given two points. The graph on the right has two points (-4, -3) and (4, -3) plotted on a coordinate plane. The solution uses the slope formula and point-slope form to derive the equation. The slope is calculated as 0, indicating a horizontal line. The final equation is y = -3. The task is to find the equation of a line given two points (-4, -3) and (4, -3). The slope is computed using the formula (y2 - y1) / (x2 - x1), resulting in 0. Since the slope is 0, the line is horizontal. Using the point-slope form y - y1 = m(x - x1), the equation is simplified to y = -3. This indicates a horizontal line passing through y = -3.
Horizontal lines represent a special case in linear functions where the y-coordinate remains constant regardless of the x-coordinate. This example helps students understand that when the slope is zero, the resulting equation is always in the form y = (constant). Recognizing and interpreting horizontal lines is crucial in various real-world applications, such as constant rates or unchanging values over time.
Exposure to special cases like horizontal lines enhances students' overall comprehension of linear functions. This example reinforces the concept that not all linear relationships involve changing y-values, broadening students' perspective on what constitutes a linear function. Such diverse examples prepare students for more complex mathematical concepts and improve their ability to model real-world scenarios mathematically.
Teacher's Script: Here we have another special case: a horizontal line. Notice that both points have the same y-coordinate. What happens to our slope when we calculate it? That's right, we get zero! This means our line doesn't rise or fall as x changes. Our equation simplifies to just y = -3. Remember, horizontal lines always have a slope of zero and an equation in the form y = (constant). Think about real-life situations where a horizontal line might represent something important, like a constant speed or a fixed price.
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.6, CCSS.MATH.CONTENT.8.EE.B.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Point-Slope Form • Slope-Intercept Form |
| Copyright Year | 2013 |
| Keywords | point-slope form, slope-intercept form, linear equations |