Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8
Display Title
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8
Topic
Linear Functions
Description
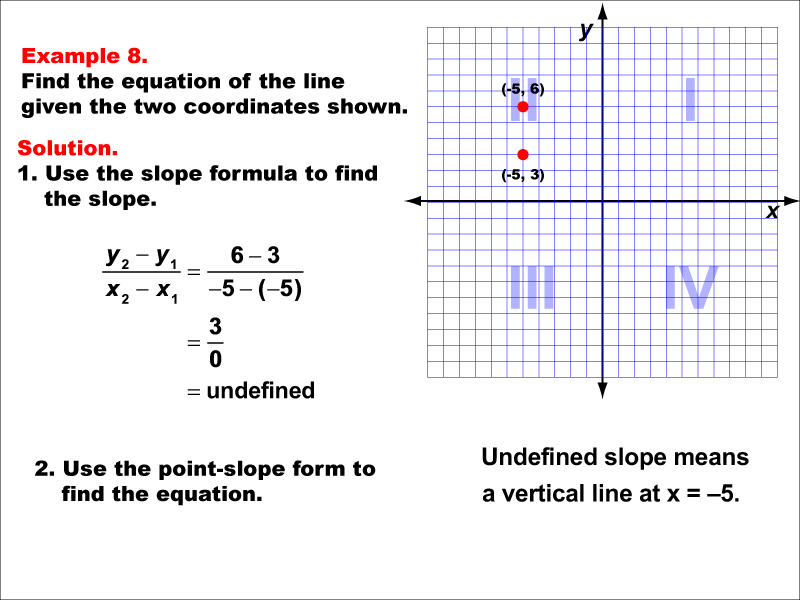
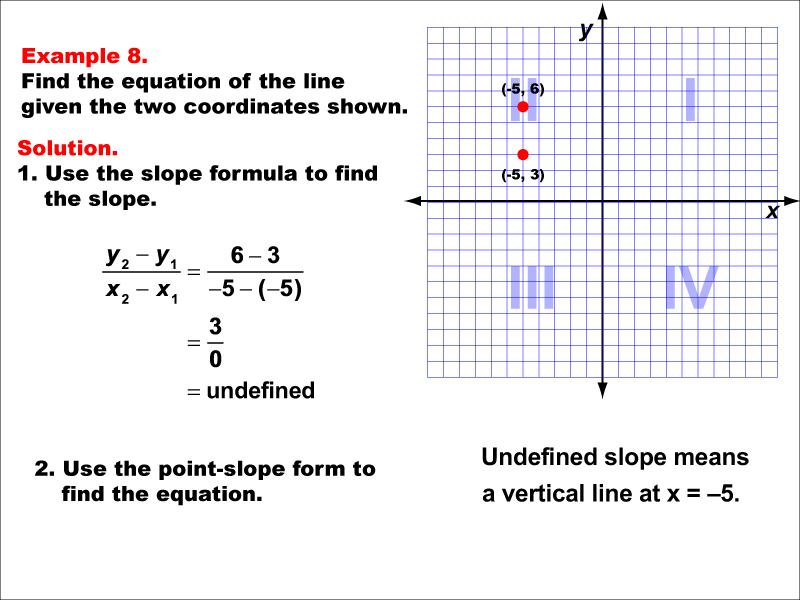
This image shows a graph with two points (-5, 6) and (-5, 3). The slope is undefined because the x-values are equal. This results in a vertical line at x = -5. The slope is undefined, indicating a vertical line at x = -5.
Linear functions are a cornerstone of algebraic concepts and have wide-ranging applications in real-world scenarios. This collection of examples serves to reinforce the understanding of linear functions by presenting various cases, including positive and negative slopes, as well as special cases like horizontal and vertical lines. By exploring different situations, students can develop a robust comprehension of determining line equations from given points.
The importance of multiple worked-out examples in mathematics education cannot be overstated. Each example in this collection provides students with an opportunity to practice the steps involved in finding a line's equation, while also exposing them to different scenarios they might encounter. This repetition helps solidify their understanding and builds their confidence in tackling similar problems independently.
Teacher's Script: Now, let's examine our eighth example. We have two points: (-5, 6) and (-5, 3). What do you notice about their x-coordinates? Exactly, they're the same! This is another special case that results in a vertical line. We can't use our usual slope formula here because it would involve dividing by zero. Let's see how we handle this unique situation and what it means for our equation.
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.6, CCSS.MATH.CONTENT.8.EE.B.5 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Point-Slope Form • Slope-Intercept Form |
| Copyright Year | 2013 |
| Keywords | point-slope form, slope-intercept form, linear equations |