Display Title
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5
Display Title
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 5
Topic
Linear Functions
Description
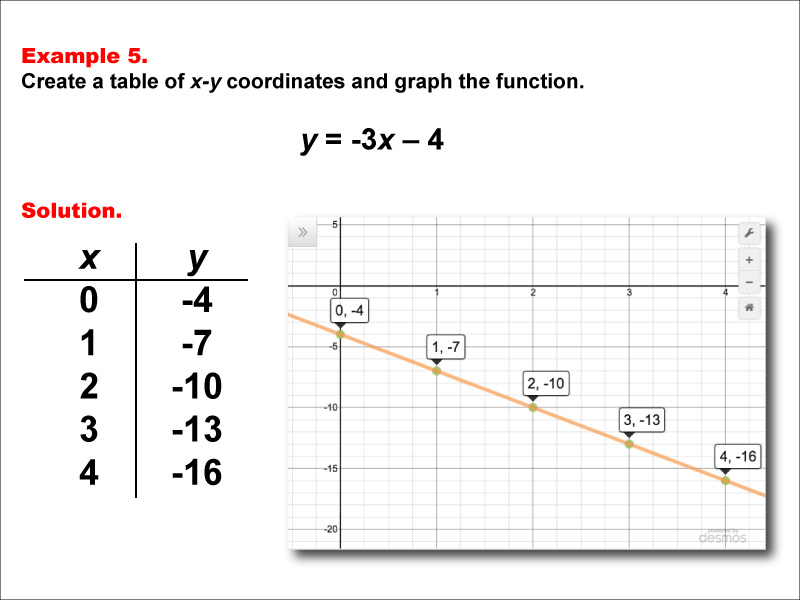
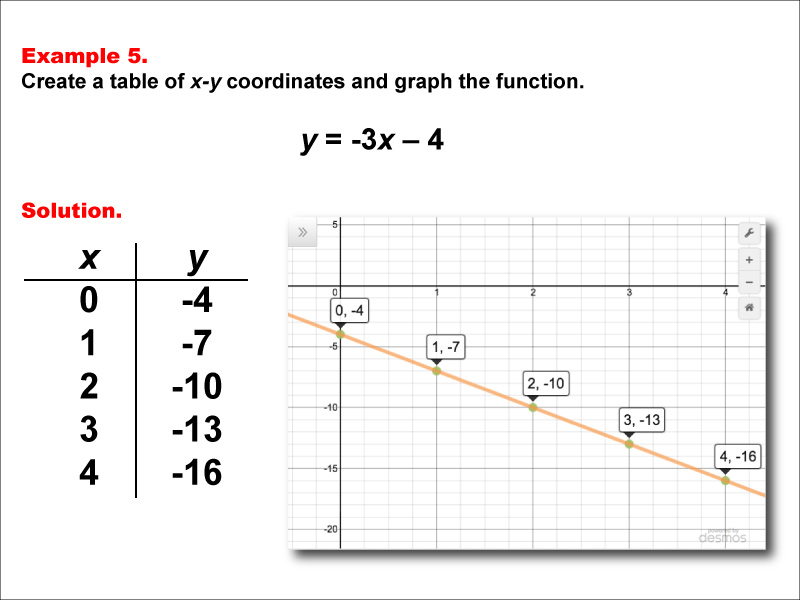
This example illustrates the creation of a table of x-y coordinates and the graphing of the linear function y = -3x - 4. The image displays both a graph and a table representing this function. The table includes coordinate pairs (0, -4), (1, -7), (2, -10), (3, -13), and (4, -16), showing how the y-value decreases by 3 for each unit increase in x.
Linear functions are a key concept in algebra, representing relationships where the rate of change between variables is constant. This collection of examples helps teach this topic by providing visual representations of various linear functions, allowing students to see how changes in the equation affect the graph and table of values.
Exposure to multiple worked-out examples is essential for students to fully grasp the concept of linear functions. By examining different slopes, including steeper negative slopes, y-intercepts, and various combinations of these elements, students can develop a more comprehensive understanding of how these components influence the function's behavior.
Teacher's Script: Let's examine the function y = -3x - 4. How does this function compare to our previous examples? Notice the steeper negative slope and the negative y-intercept. How do these elements affect our graph and our table of values? Can you predict what the next point in our table would be?
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions in Tabular and Graph Form Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.EE.C.9, CCSS.MATH.CONTENT.8.F.A.3 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Graphs of Linear Functions |
| Copyright Year | 2015 |
| Keywords | function, linear functions, graphs of linear functions, function tables |