Display Title
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6
Display Title
Math Example--Linear Function Concepts--Linear Functions in Tabular and Graph Form: Example 6
Topic
Linear Functions
Description
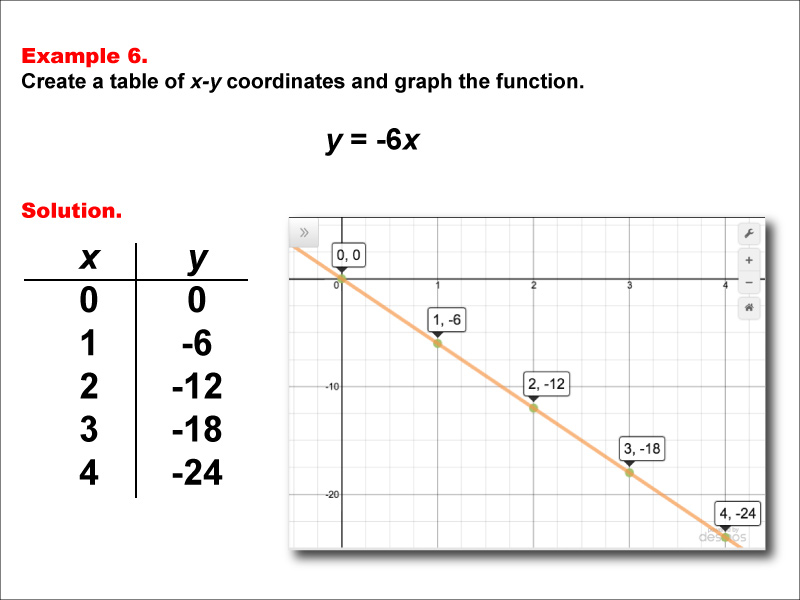
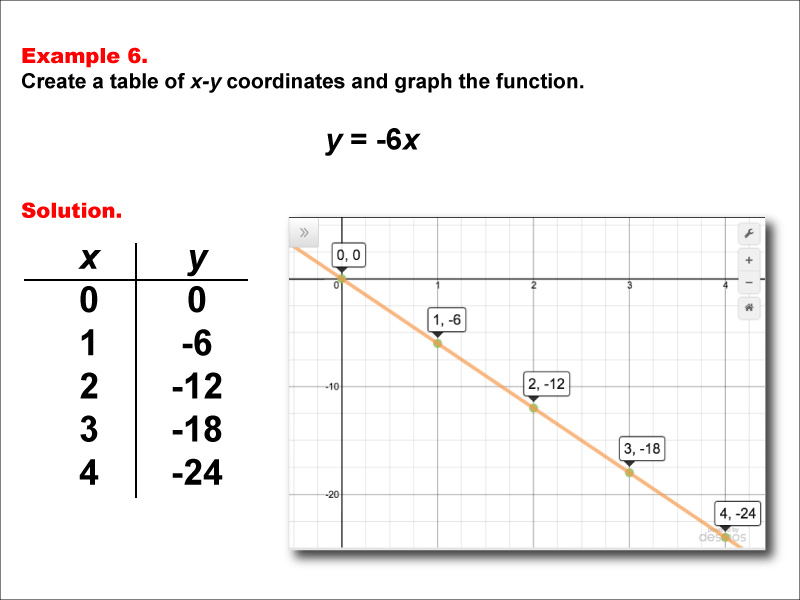
This example demonstrates how to create a table of x-y coordinates and graph the linear function y = -6x. The image shows both a graph and a table representing this function. The table includes coordinate pairs (0, 0), (1, -6), (2, -12), (3, -18), and (4, -24), illustrating how the y-value decreases by 6 for each unit increase in x.
Linear functions are a fundamental concept in algebra, representing relationships where the rate of change between variables is constant. This collection of examples helps teach this topic by providing visual representations of various linear functions, allowing students to see how changes in the equation affect the graph and table of values.
Exposure to multiple worked-out examples is crucial for students to fully grasp the concept of linear functions. By seeing different slopes, including steep negative slopes, and special cases like this one where the y-intercept is 0, students can develop a more comprehensive understanding of how these elements influence the function's behavior.
Teacher's Script: Now, let's analyze the function y = -6x. What's unique about this function compared to our previous examples? Notice the steep negative slope and the absence of a constant term. How does this affect our graph and our table of values? Can you explain why the line passes through the origin (0, 0)?
For a complete collection of math examples related to Linear Functions click on this link: Math Examples: Linear Functions in Tabular and Graph Form Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.EE.C.9, CCSS.MATH.CONTENT.8.F.A.3 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Graphs of Linear Functions |
| Copyright Year | 2015 |
| Keywords | function, linear functions, graphs of linear functions, function tables |