Display Title
Math Example--Linear Function Concepts--Parallel and Perpendicular Lines: Example 1
Display Title
Math Example--Linear Function Concepts--Parallel and Perpendicular Lines: Example 1
Topic
Linear Functions
Description
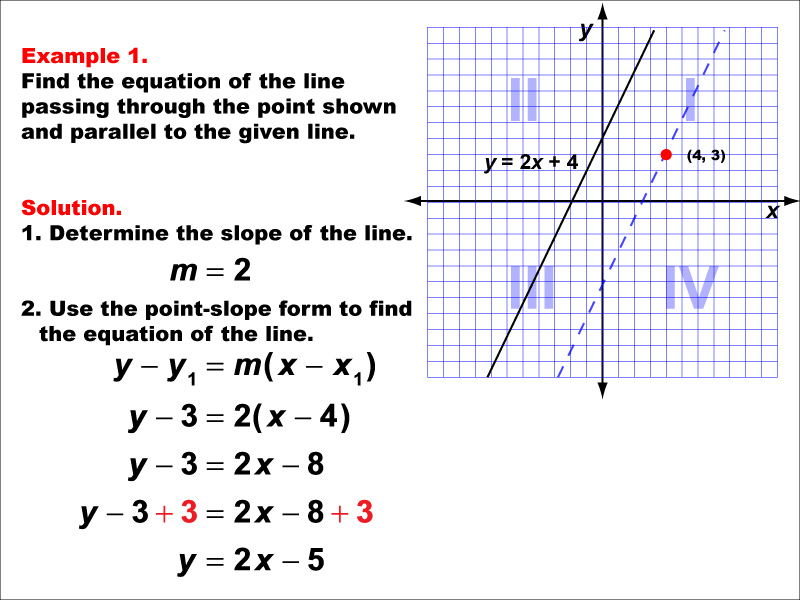
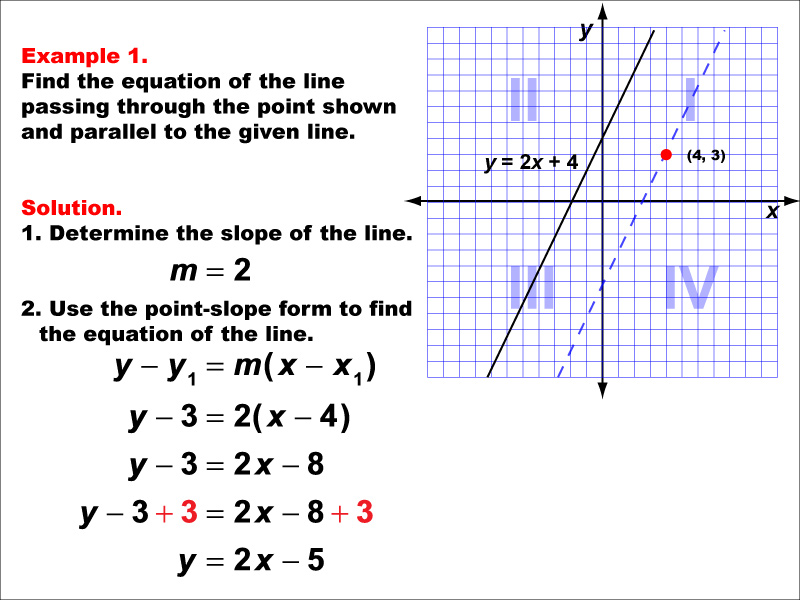
This example demonstrates how to find the equation of a line parallel to y = 2x + 4 and passing through the point (4, 3). The solution involves using the slope m = 2 and applying the point-slope form of a line equation. The resulting equation is y - 3 = 2(x - 4), which simplifies to y = 2x - 5.
Understanding parallel and perpendicular lines is crucial in linear functions. These examples help students grasp the relationship between slopes of parallel lines and how to use given information to derive new line equations. The visual representation of the problem on a graph aids in comprehending the spatial relationship between the given line and the point.
Multiple worked-out examples are essential for students to fully understand this concept. They provide various scenarios and reinforce the application of slope and point-slope form in different contexts. This repetition helps solidify the process and improves problem-solving skills.
Teacher's Script: Today, we'll learn how to find equations of lines parallel to a given line. Remember, parallel lines have the same slope. Let's use the slope of the given line and the point-slope form to create our new equation.
For a complete collection of math examples related to Parallel and Perpendicular Lines click on this link: Math Examples: Equations of Parallel and Perpendicular Lines Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines • Perpendicular Lines |
| Copyright Year | 2013 |
| Keywords | parallel lines, perpendicular lines |