Display Title
Math Example--Linear Function Concepts--Parallel and Perpendicular Lines: Example 13
Display Title
Math Example--Linear Function Concepts--Parallel and Perpendicular Lines: Example 13
Topic
Linear Functions
Description
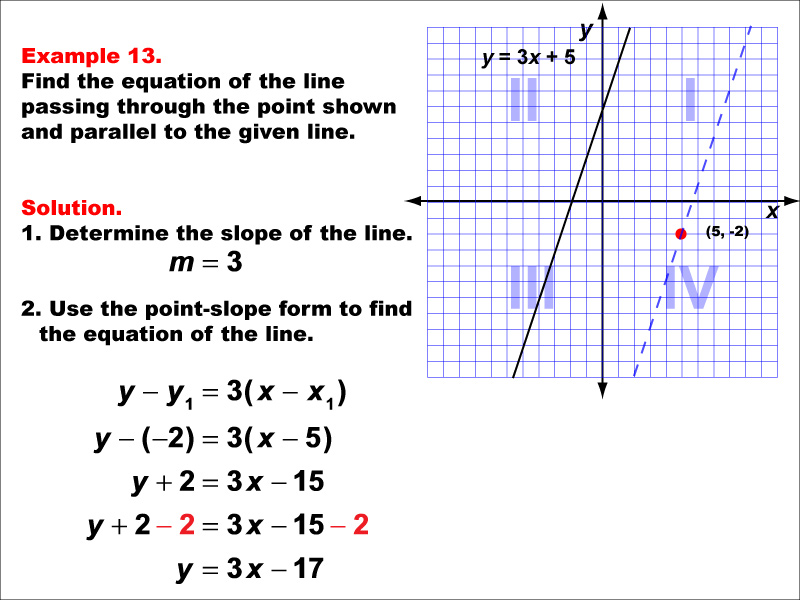
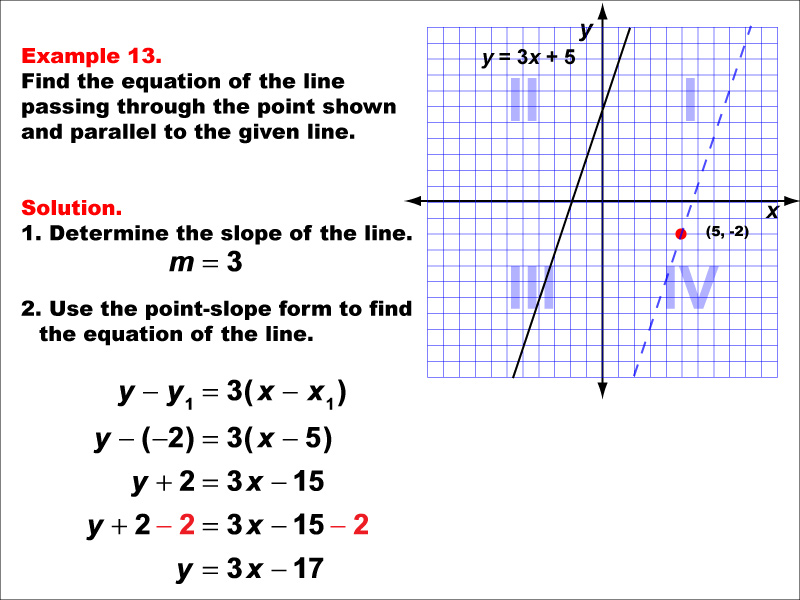
This example demonstrates how to find the equation of a line parallel to y = 3x + 5 and passing through the point (5, -2). The solution involves using the slope m = 3 and applying the point-slope form. The resulting equation is y - (-2) = 3(x - 5), which simplifies to y = 3x - 17.
Understanding parallel lines is fundamental in linear functions. These examples help students grasp the concept that parallel lines have the same slope and how to use this information along with a given point to derive new line equations. The visual representation on a graph aids in comprehending the spatial relationship between the given line and the parallel line.
Providing multiple worked-out examples is crucial for students to fully understand this concept. They offer various scenarios and reinforce the application of slope and point-slope form in different contexts. This repetition helps solidify the process and improves problem-solving skills.
Teacher's Script: Let's continue our practice with parallel lines. Remember, parallel lines always have the same slope. We'll use the slope of the given line and the point-slope form to create our new equation. Pay attention to how we handle negative y-coordinates in the point-slope form.
For a complete collection of math examples related to Parallel and Perpendicular Lines click on this link: Math Examples: Equations of Parallel and Perpendicular Lines Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines • Perpendicular Lines |
| Copyright Year | 2013 |
| Keywords | parallel lines, perpendicular lines |