Display Title
Math Example--Linear Function Concepts--Parallel and Perpendicular Lines: Example 6
Display Title
Math Example--Linear Function Concepts--Parallel and Perpendicular Lines: Example 6
Topic
Linear Functions
Description
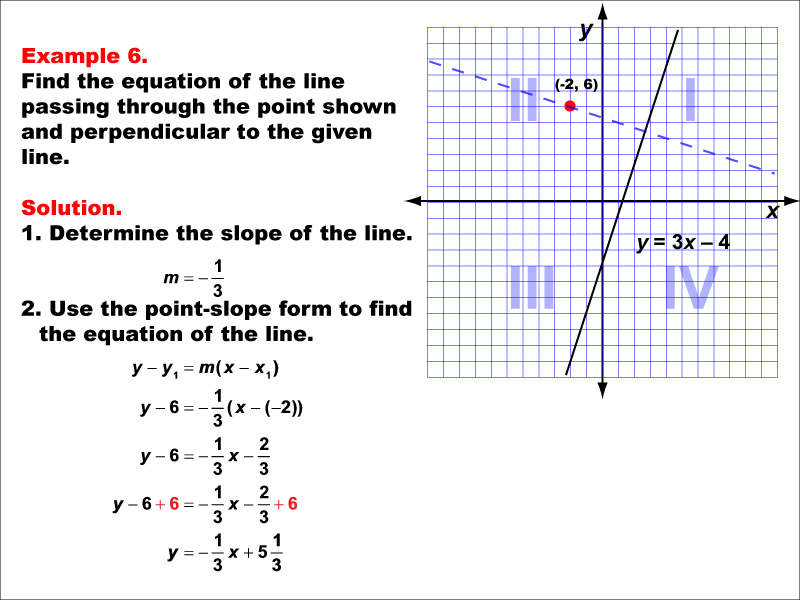
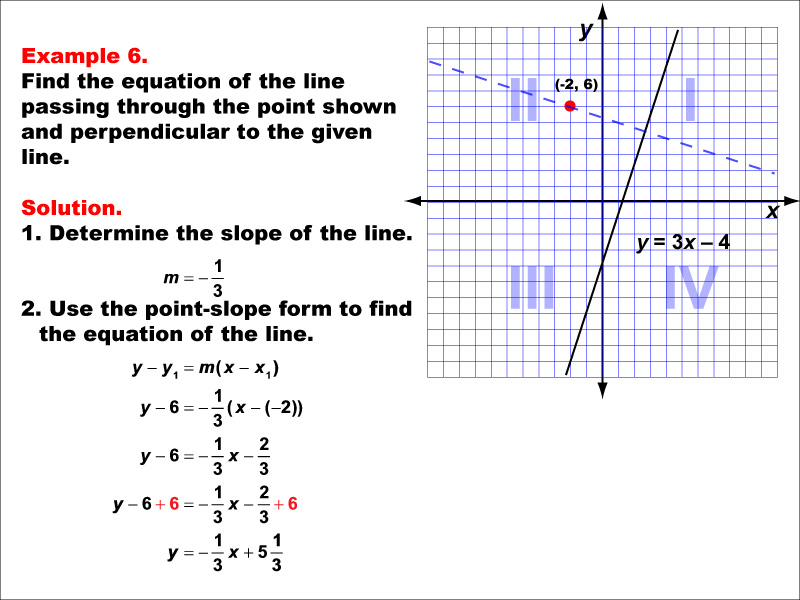
This example illustrates how to find the equation of a line passing through the point (-2, 6) and perpendicular to y = 3x - 4. The solution uses the negative reciprocal slope m = -1/3 and applies the point-slope form. The resulting equation is y - 6 = -1/3(x + 2), which simplifies to y = -1/3x + 5 + 1/3.
Understanding perpendicular lines is crucial in linear functions. These examples help students grasp the concept that perpendicular lines have slopes that are negative reciprocals of each other and how to use this information along with a given point to derive new line equations. The visual representation on a graph aids in comprehending the spatial relationship between the given line and the perpendicular line.
Exposure to multiple worked-out examples is essential for students to fully understand this concept. They provide various scenarios and reinforce the application of negative reciprocal slopes and point-slope form in different contexts. This repetition helps solidify the process and improves problem-solving skills.
Teacher's Script: Now, let's practice finding equations of perpendicular lines again. Remember, the slopes of perpendicular lines are negative reciprocals of each other. We'll use this principle along with the point-slope form to create our new equation. Notice how we handle fractions in the slope and simplify the final equation.
For a complete collection of math examples related to Parallel and Perpendicular Lines click on this link: Math Examples: Equations of Parallel and Perpendicular Lines Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.B.5 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines • Perpendicular Lines |
| Copyright Year | 2013 |
| Keywords | parallel lines, perpendicular lines |