Display Title
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4
Display Title
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4
Topic
The Point-Slope Form
Description
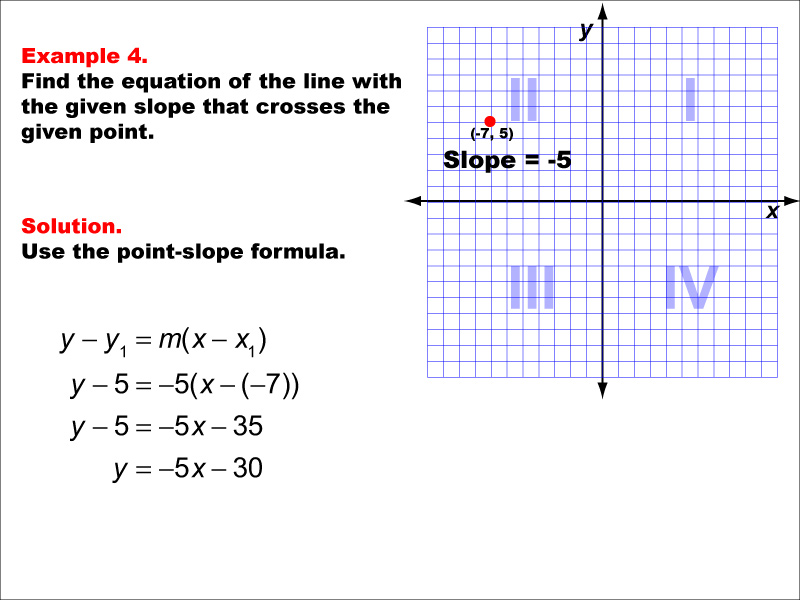
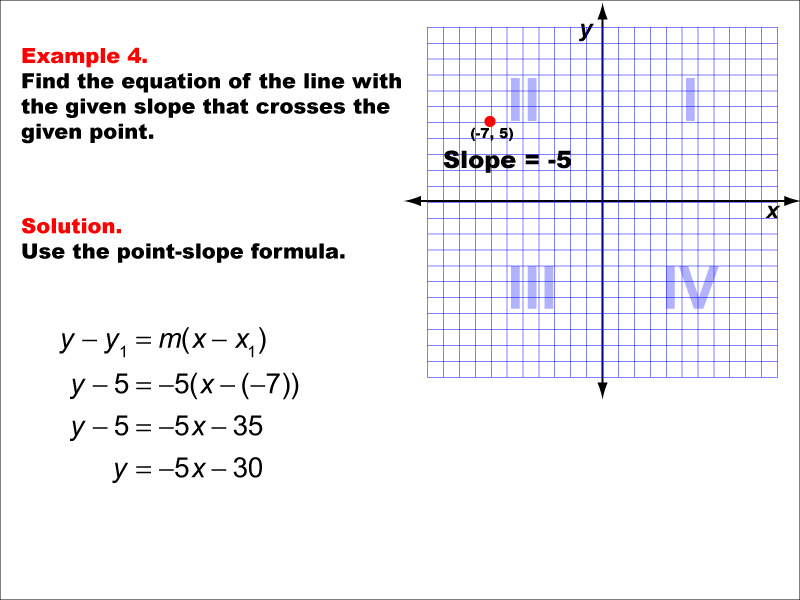
In this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30.
The point-slope form is a powerful tool in linear algebra, enabling us to quickly determine the equation of a line given a point and its slope. This collection of examples helps illustrate the formula's application across various scenarios, reinforcing students' understanding of how to use it with different numerical values and graph positions.
Providing multiple worked-out examples is essential for students to fully comprehend the point-slope form concept. Each example presents a unique combination of slope and point coordinates, allowing learners to practice applying the formula in different contexts. This approach helps solidify understanding and builds problem-solving confidence.
Teacher's Script: Let's move on to our fourth example. We have a line with a slope of -5 that goes through the point (-7, 5). Can you remind me of our point-slope formula? Excellent! It's y - y1 = m(x - x1). Now, let's work together to identify which values go where in this formula. Pay attention to how we handle the negative slope and x-coordinate. Let's simplify our equation step by step to find the final form of our line.
For a complete collection of math examples related to the Point-Slope Form click on this link: Math Examples: Point-Slope Form Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.6, CCSS.MATH.CONTENT.8.EE.B.5 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Point-Slope Form |
| Copyright Year | 2013 |
| Keywords | point-slope form, slope-intercept form, linear equations |