Display Title
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 3
Display Title
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 3
Topic
Measures of Central Tendency
Description
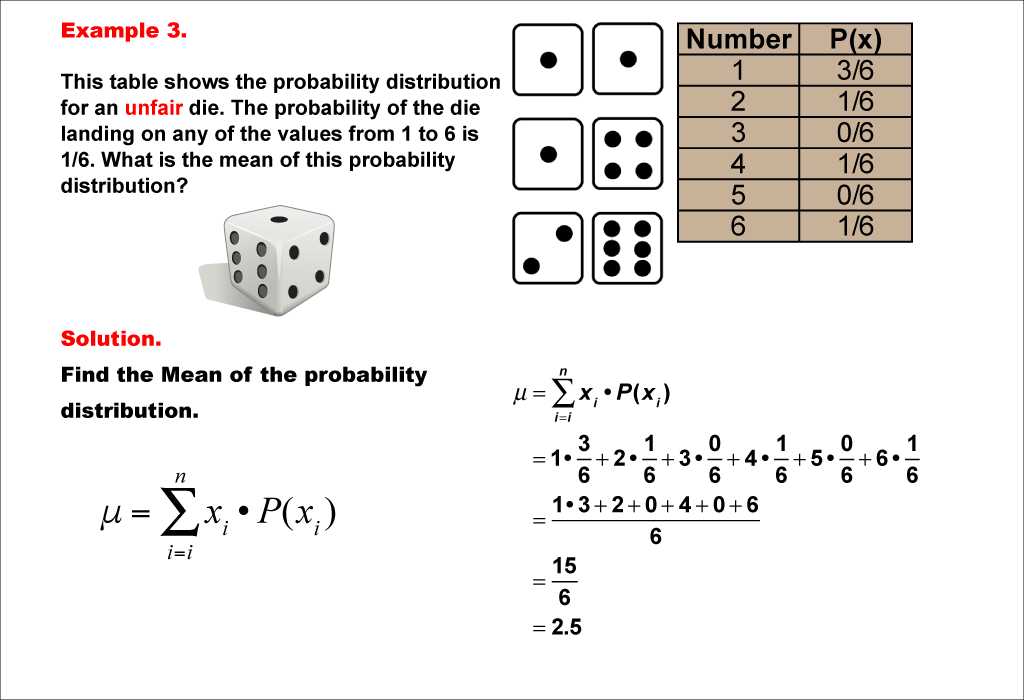
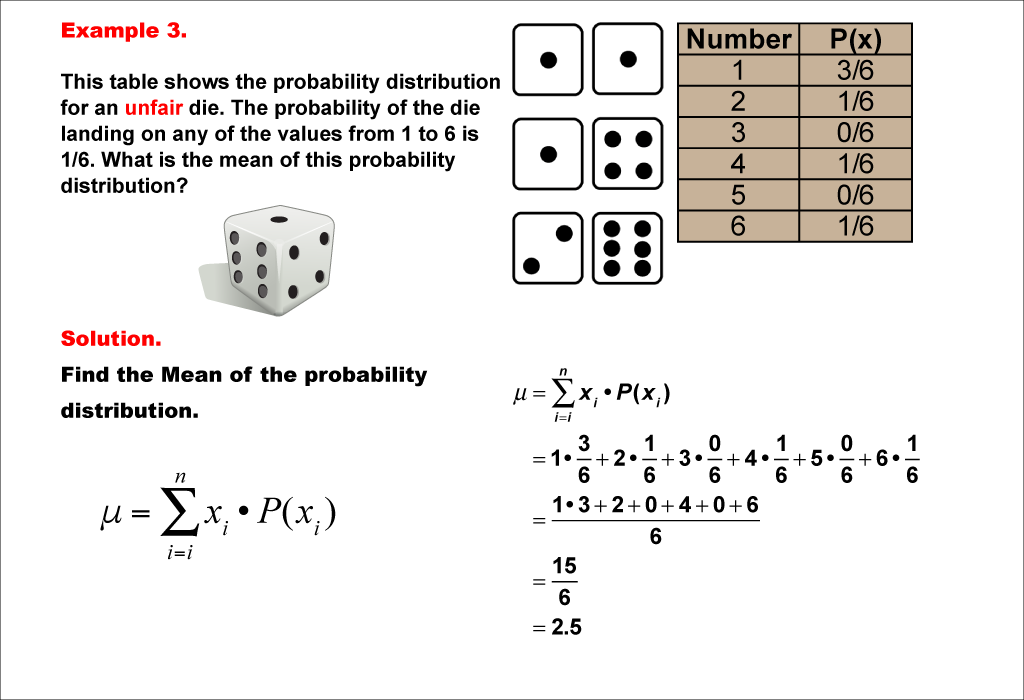
This example demonstrates the calculation of the mean for another unfair six-sided die. In this case, the probability of rolling a 1 is even higher (3/6), while some numbers have a probability of 0. The mean is calculated using the same method, resulting in 2.5.
The collection of examples on measures of central tendency, particularly the mean of probability distributions, helps students understand how to calculate and interpret expected values in various scenarios. By presenting different probability distributions, students can observe how changes in probabilities affect the mean and gain insight into the concept of expected value in random events.
Providing multiple worked-out examples is essential for students to fully grasp this concept. Each example introduces a new variation in probability distribution, allowing students to apply the same calculation method to different scenarios. This repetition helps reinforce their understanding and improves their ability to solve similar problems independently.
Teacher's Script: Let's look at another unfair die. This time, notice how some numbers have a probability of 0, meaning they can't occur at all. How do you think this will affect our mean? We'll use the same calculation method, but pay close attention to how these extreme probabilities influence our result. Can you explain why the mean might be lower in this case compared to our previous examples?
For a complete collection of math examples related to Measures of Central Tendency click on this link: Math Examples: Measures of Central Tendency: Mean of a Probability Distribution Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.SP.A.2 |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Probability and Data Analysis • Data Analysis |
| Copyright Year | 2021 |
| Keywords | mean, measures of central tendency |