Display Title
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 5
Display Title
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 5
Topic
Measures of Central Tendency
Description
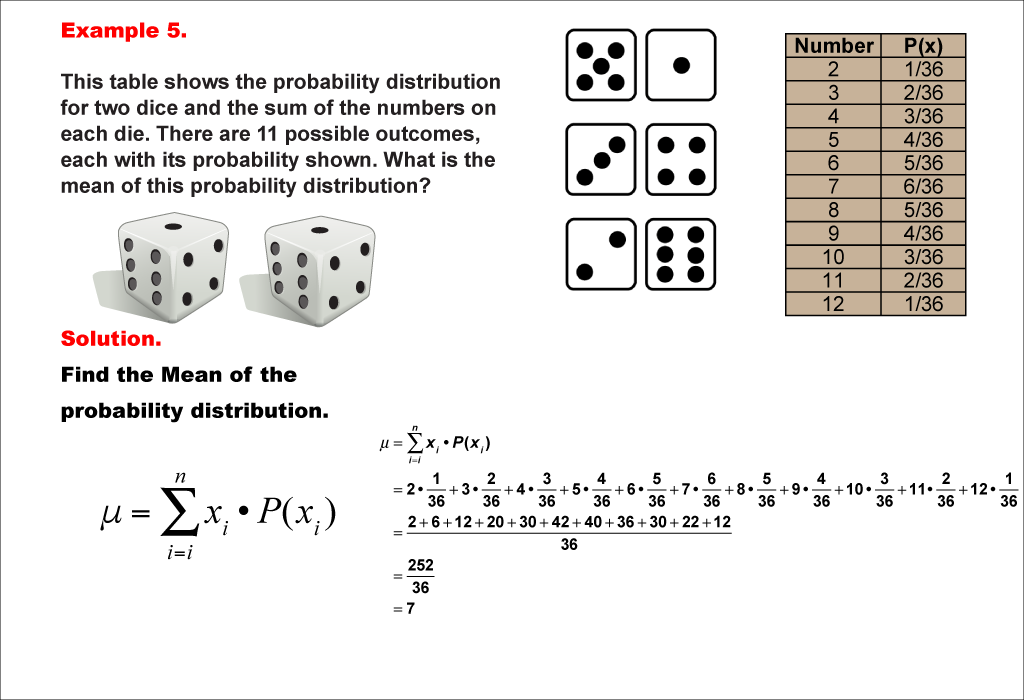
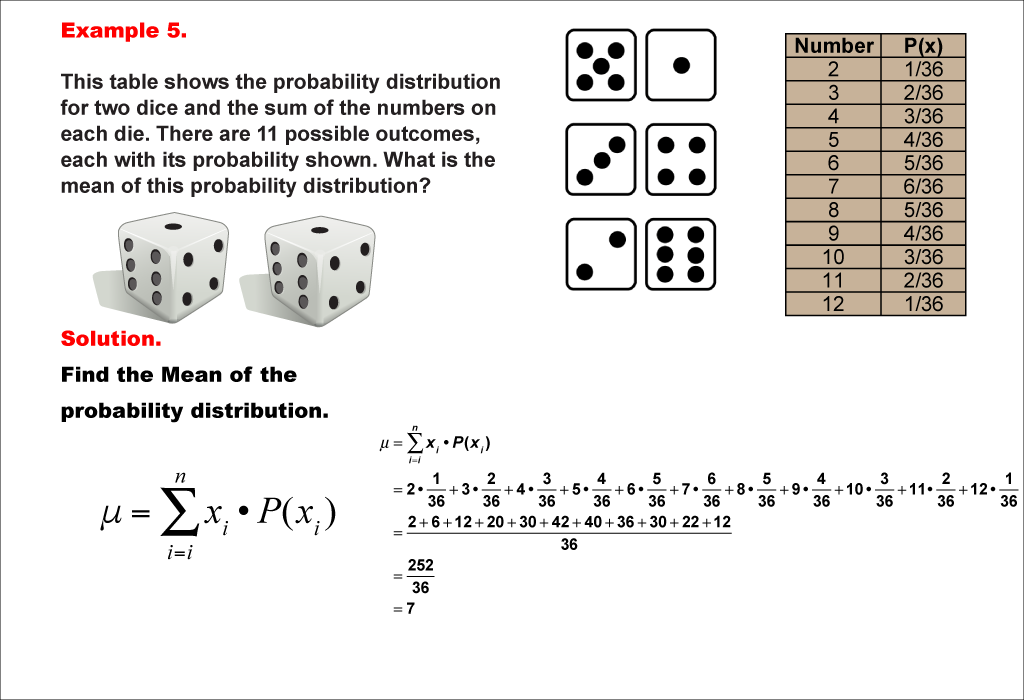
This example demonstrates the calculation of the mean for the probability distribution of the sum when rolling two fair dice. There are 11 possible outcomes (2 to 12), each with its own probability. The mean is calculated using the same method as previous examples, resulting in 7.
This collection of examples on measures of central tendency, particularly the mean of probability distributions, helps students understand how to calculate and interpret expected values in increasingly complex scenarios. By progressing from single dice to multiple dice, students can observe how combining random events affects probability distributions and means.
Providing multiple worked-out examples is essential for students to fully grasp this concept. Each example builds upon the previous ones, allowing students to apply their knowledge to more complex situations. This progression helps reinforce their understanding and improves their ability to analyze and solve probability problems in various contexts.
Teacher's Script: Now let's look at a more complex scenario: rolling two dice and finding the mean of their sum. Notice how we have more possible outcomes now, each with its own probability. Can you see why some sums are more likely than others? Let's calculate the mean together. How does this result compare to what you might have intuitively expected for the average sum of two dice?
For a complete collection of math examples related to Measures of Central Tendency click on this link: Math Examples: Measures of Central Tendency: Mean of a Probability Distribution Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.SP.A.2 |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Probability and Data Analysis • Data Analysis |
| Copyright Year | 2021 |
| Keywords | mean, measures of central tendency |