Display Title
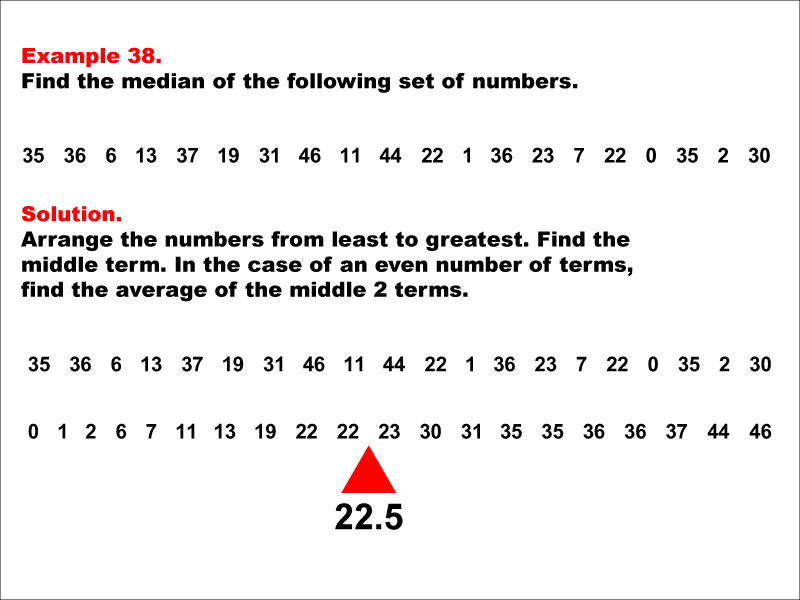
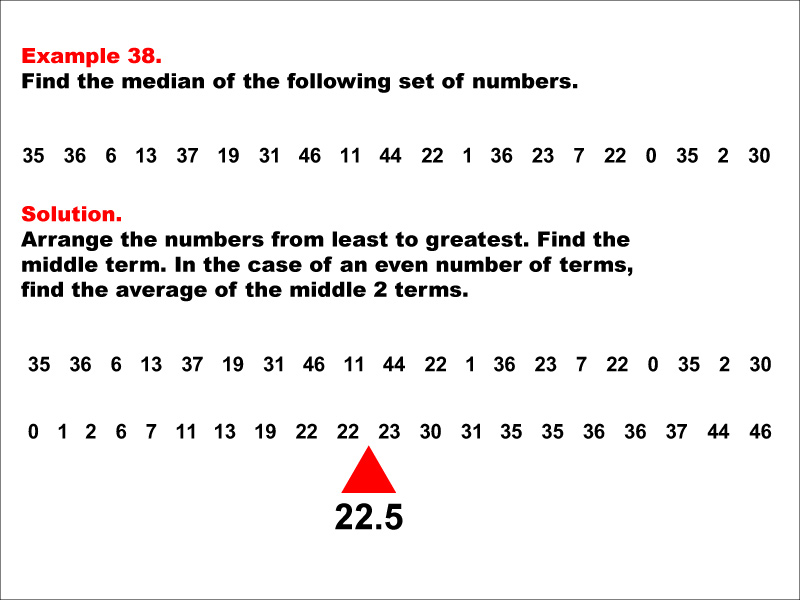
Math Example--Measures of Central Tendency--Median: Example 38
Display Title
Math Example--Measures of Central Tendency--Median: Example 38
Topic
Measures of Central Tendency
Description
This example demonstrates finding the median of the following set of numbers: 3, 5, 1, 4, 2. The solution involves arranging the numbers from least to greatest and then identifying the middle value. With an odd number of terms, the median is simply the middle number after sorting, which is 3.
The concept of median is a fundamental measure of central tendency in statistics. It represents the middle value in a sorted dataset, providing a robust measure that is less affected by extreme values compared to the mean. This collection of examples helps teach the topic by illustrating the step-by-step process of finding the median for various datasets, including those with small sets of numbers.
Presenting multiple worked-out examples is crucial for students to fully grasp the concept of median. By encountering different scenarios, such as datasets with even or odd numbers of values, students can develop a comprehensive understanding of how to calculate the median in various situations. This approach reinforces the procedure and helps students recognize patterns and nuances in median calculation.
Teacher Script: "Let's look at this small set of numbers. Remember, our first step is always to arrange the numbers from least to greatest. Once we've sorted our numbers, finding the median is straightforward since we have an odd number of terms. It's simply the middle number in our ordered list. This example shows how the median works with a small dataset, giving us the central value that represents the middle of our data."
For a complete collection of math examples related to Measures of Central Tendency click on this link: Math Examples: Measures of Central Tendency: Median Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.SP.B.4, CCSS.MATH.CONTENT.6.SP.A.3, CCSS.MATH.CONTENT.HSS.ID.A.2, CCSS.MATH.CONTENT.HSS.ID.A.3 |
|---|---|
| Grade Range | 6 - 12 |
| Curriculum Nodes |
Algebra • Probability and Data Analysis • Data Analysis |
| Copyright Year | 2014 |
| Keywords | data analysis, tutorials, measures of central tendency, median, average |