Display Title
Math Example--Measures of Central Tendency--Weighted Mean--Example 6
Display Title
Math Example--Measures of Central Tendency--Weighted Mean--Example 6
Topic
Measures of Central Tendency
Description
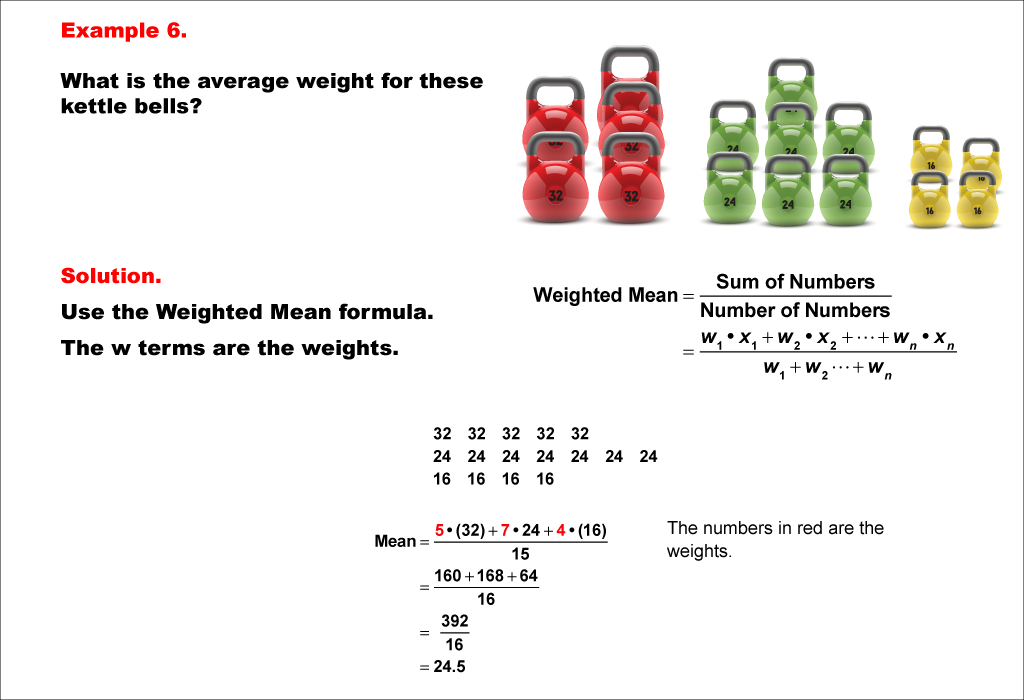
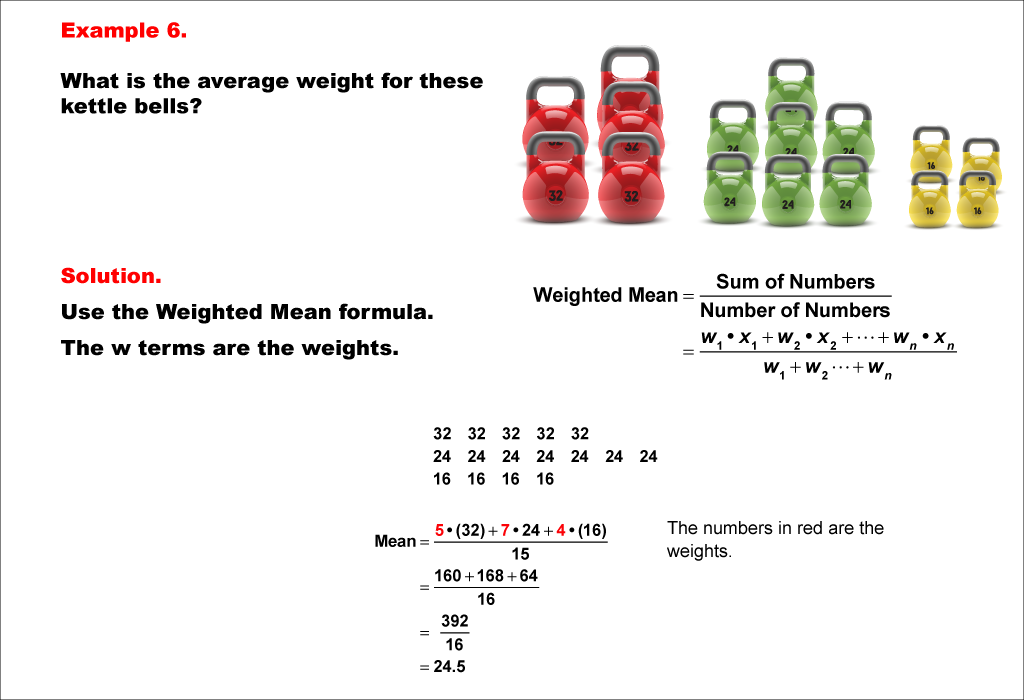
This example illustrates another real-world application of weighted mean, using kettlebells of different weights: 32, 24, and 16 pounds, with quantities of 5, 7, and 4 respectively. The weighted mean is computed using the formula: (5 * 32 + 7 * 24 + 4 * 16) / (5 + 7 + 4), resulting in an average weight of 24.5 pounds.
Weighted mean is a vital concept in measures of central tendency, allowing for the consideration of the relative frequency or quantity of each data point. This collection of examples helps teach this topic by providing practical scenarios, such as calculating the average weight of kettlebells with different quantities, enabling students to understand the application of the weighted mean formula in tangible, real-world contexts.
Presenting multiple worked-out examples, particularly those with practical applications, is essential for students to fully comprehend the concept of weighted mean. By observing the formula applied to diverse situations, students can develop a deeper understanding of how weights influence the final average and how to interpret the results in everyday scenarios they might encounter.
Teacher's Script: Here's another example using kettlebells, but with different quantities. How does this change in quantities affect our result compared to the previous example? Can you think of a situation in your daily life where you might need to calculate a weighted average?
For a complete collection of math examples related to Measures of Central Tendency click on this link: Math Examples: Measures of Central Tendency: Weighted Mean Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.SP.B.5.C |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Probability and Data Analysis • Data Analysis |
| Copyright Year | 2021 |
| Keywords | mean, measures of central tendency |