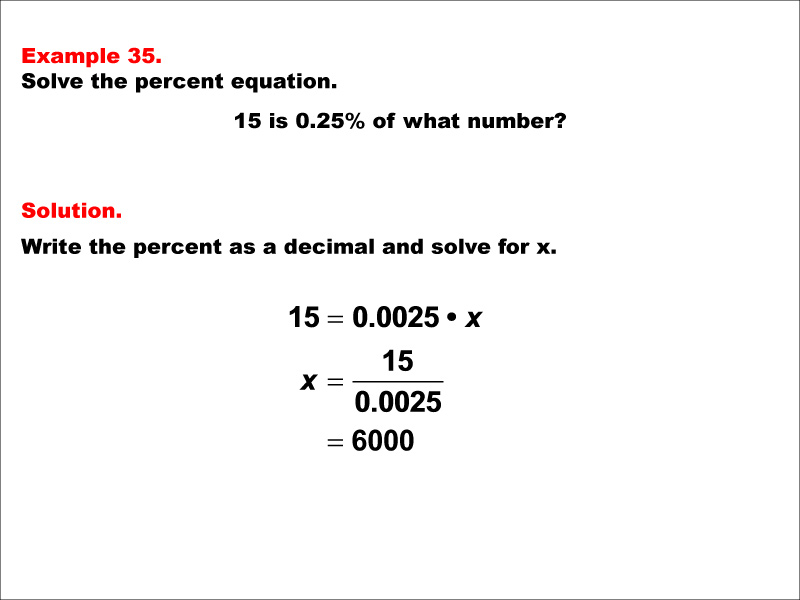
Display Title
Math Example--Percents--Equations with Percents: Example 35
Display Title
Math Example--Percents--Equations with Percents: Example 35
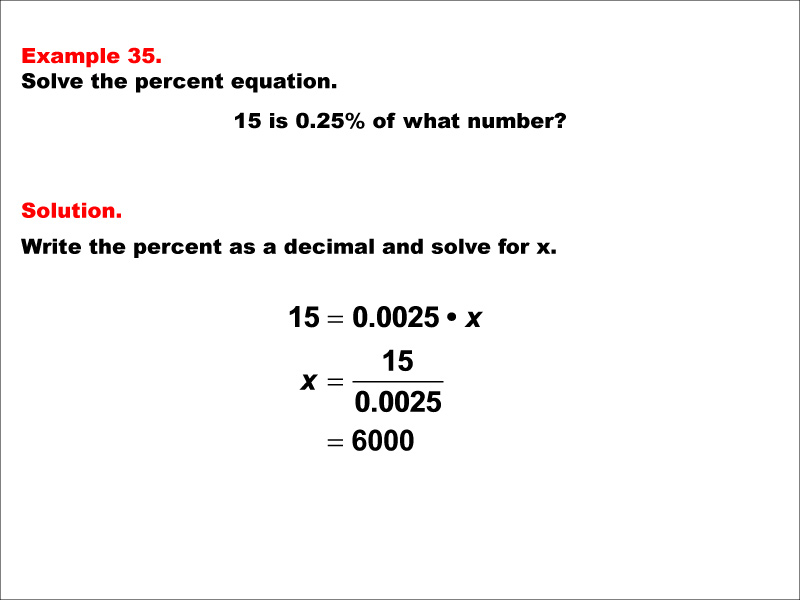
Topic
Solving Equations
Description
This math example demonstrates solving percent equations by asking "15 is 0.25% of what number?" The solution involves setting up the equation 15 = 0.0025 * x, then solving for x to get x = 15 / 0.0025, which equals 6000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value.
Solving equations with percents is a fundamental skill in mathematics that has wide-ranging applications in finance, statistics, and data analysis. These examples help students understand how to set up and solve equations involving percentages, especially in cases where we are dealing with very small percentages. This skill is crucial for more advanced mathematical concepts and real-world problem-solving scenarios, such as calculating total populations from small samples, estimating large quantities from minor measurements, or understanding scale in various contexts where we deal with minute proportions.
The importance of presenting multiple worked-out examples cannot be overstated. Each new example reinforces the concept while introducing different scenarios, including those where we work with very small percentages to find much larger wholes. This approach helps students recognize patterns, adapt their problem-solving strategies, and gain confidence in their ability to handle diverse percentage-based calculations. By practicing with various value pairs, students develop a more comprehensive understanding of how percentages relate different quantities and prepare for more complex mathematical challenges they may encounter in higher education or professional settings.
Teacher Script: "Let's tackle this challenging percent problem. We're asked, '15 is 0.25% of what number?' To solve this, we first convert 0.25% to a decimal, which is 0.0025. Then we set up the equation 15 = 0.0025 * x. Now, how do we solve for x? We divide both sides by 0.0025. This gives us x = 15 / 0.0025, which equals 6000. Notice that our result is significantly larger than the given number 15. This is because 0.25% is a very small fraction of the whole, so the whole must be much larger. In real-world scenarios, you might encounter situations where you need to estimate a total from a very small percentage. For example, if 15 rare artifacts represent 0.25% of all artifacts in a large archaeological site, you could calculate that there are 6000 artifacts in total. Understanding these concepts is crucial for analyzing large-scale data, estimating populations from small samples, and interpreting proportions in various fields like archaeology, epidemiology, or statistical analysis where we often deal with very small percentages of much larger wholes."
For a complete collection of math examples related to Solving Equations click on this link: Math Examples: Equations with Percents Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.EE.B.5, CCSS.MATH.CONTENT.7.RP.A.3, CCSS.MATH.CONTENT.6.RP.A.3.C |
|---|---|
| Grade Range | 5 - 8 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Solving Percent Equations |
| Copyright Year | 2013 |
| Keywords | Percent, equation, solution, solving equation, percentage |