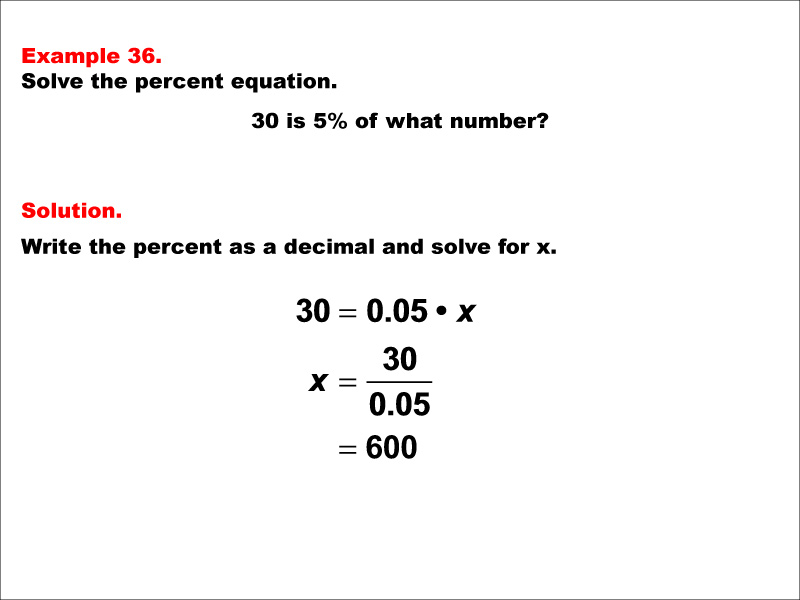
Display Title
Math Example--Percents--Equations with Percents: Example 36
Display Title
Math Example--Percents--Equations with Percents: Example 36
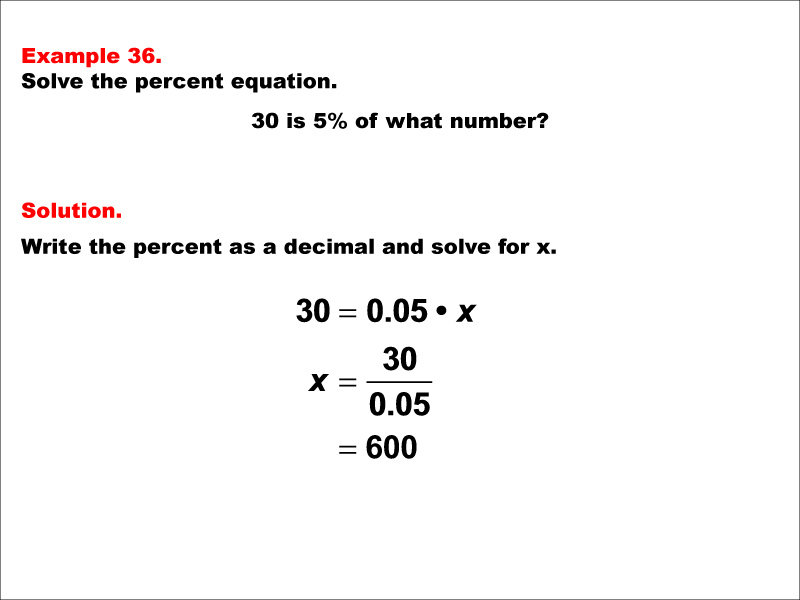
Topic
Solving Equations
Description
This math example focuses on solving percent equations by asking "30 is 5% of what number?" The solution involves setting up the equation 30 = 0.05 * x, then solving for x to get x = 30 / 0.05, which equals 600. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a much larger number.
Solving equations with percents is a critical skill in mathematics that finds applications in various fields such as finance, statistics, and data analysis. These examples help students grasp the fundamental concept of relating a small part to a much larger whole through percentages and how to set up equations to solve for unknown values. This understanding forms the basis for more complex mathematical operations and real-world problem-solving scenarios, such as calculating total populations from sample sizes, estimating large quantities from small measurements, or understanding scale in various contexts.
Providing multiple worked-out examples is essential for students to fully comprehend this concept. Each new example reinforces the process while introducing different scenarios and number relationships. This approach allows students to recognize patterns, adapt their problem-solving strategies, and build confidence in handling diverse percentage-based calculations. By practicing with various value pairs, including those that involve small percentages, students develop a more nuanced understanding of how percentages relate different quantities and prepare for more advanced mathematical challenges they may encounter in higher education or professional settings.
Teacher Script: "Let's examine this interesting percent problem. We're asked, '30 is 5% of what number?' To solve this, we first convert 5% to a decimal, which is 0.05. Then we set up the equation 30 = 0.05 * x. Now, how do we solve for x? We divide both sides by 0.05. This gives us x = 30 / 0.05, which equals 600. Notice that our result is much larger than the given number 30. This is because 5% is a small fraction, so the whole must be much larger. In real-world scenarios, you might encounter situations where you need to estimate a total from a small percentage. For example, if 30 students in a school represent 5% of the total student body, you could calculate that the school has 600 students in total. Understanding these concepts is crucial for analyzing large-scale data, estimating populations from samples, and interpreting proportions in various fields like scientific research, demographic studies, or market analysis."
For a complete collection of math examples related to Solving Equations click on this link: Math Examples: Equations with Percents Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.EE.B.5, CCSS.MATH.CONTENT.7.RP.A.3, CCSS.MATH.CONTENT.6.RP.A.3.C |
|---|---|
| Grade Range | 5 - 8 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Solving Percent Equations |
| Copyright Year | 2013 |
| Keywords | Percent, equation, solution, solving equation, percentage |