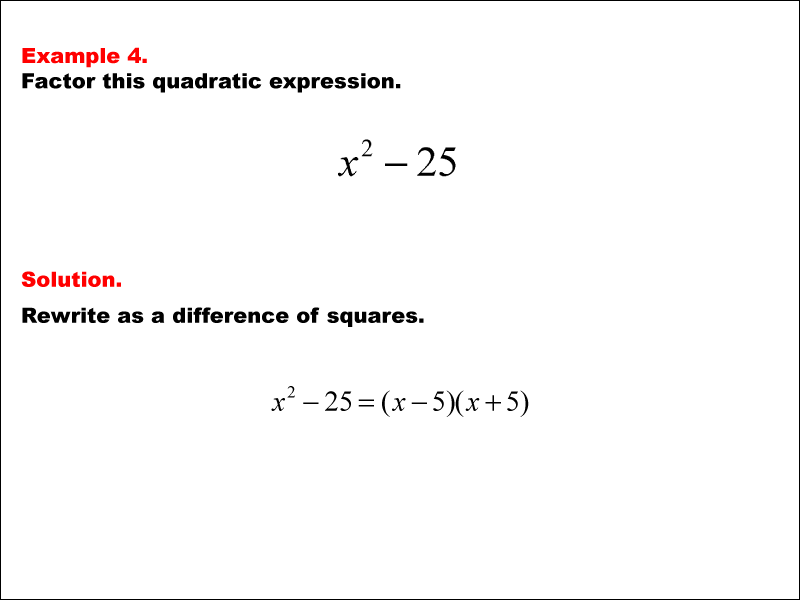
Display Title
Math Example--Polynomial Concepts--Difference of Squares and Cubes--Example 4
Display Title
Math Example--Polynomial Concepts--Difference of Squares and Cubes--Example 4
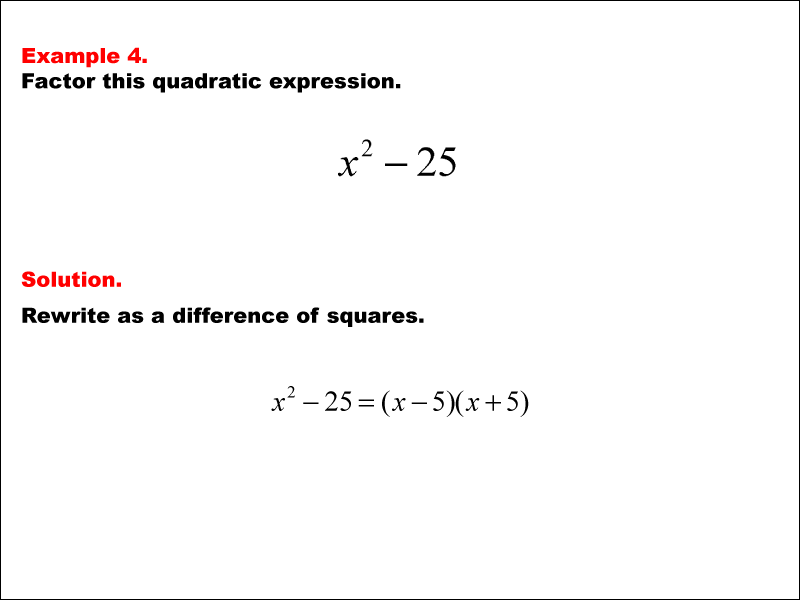
Topic
Polynomials
Description
This example shows the quadratic expression x2 - 25 being factored, labeled as 'Example 4.' The solution involves factoring it as a difference of squares.
In this example, students explore the difference of squares or cubes, helping them recognize patterns in algebraic expressions that can simplify factorization. For quadratic expressions like x2 - n, recognizing these as differences of squares allows students to factor them into two binomials. For higher degree expressions, similar methods apply, enabling the application of systematic factorization techniques.
Seeing multiple worked-out examples is crucial for students as it helps reinforce pattern recognition, deepens understanding, and builds confidence in solving such problems independently. By examining various instances, students gain familiarity with different forms and degrees of expressions, enabling them to adapt the approach to similar problems.
Teacher’s Script: Let's go over this example together. Here, we have the expression Example 4. Factor this quadratic expression. x2 - 25. Rewrite as a difference of squares. x2 - 25 = (x - 5)(x + 5). Our goal is to recognize it as a difference of squares or cubes and apply the factorization techniques we've learned. Pay close attention to each step, as understanding this process will help you tackle similar problems on your own.
For a complete collection of math examples related to Difference of Squares and Cubes click on this link: Math Examples: Difference of Squares and Cubes Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.SSE.A.1.B, CCSS.MATH.CONTENT.HSA.SSE.A.2 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Factoring Quadratics |
| Copyright Year | 2020 |
| Keywords | factoring |