Display Title
Math Example--Polynomial Concepts--Graphs of Polynomial Functions--Example 02
Display Title
Math Example--Polynomial Concepts--Graphs of Polynomial Functions--Example 02
Topic
Polynomials
Description
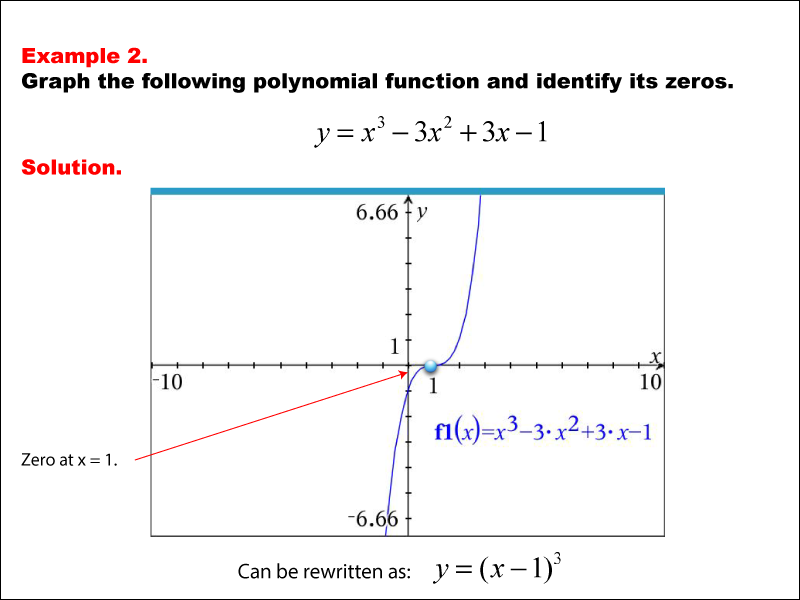
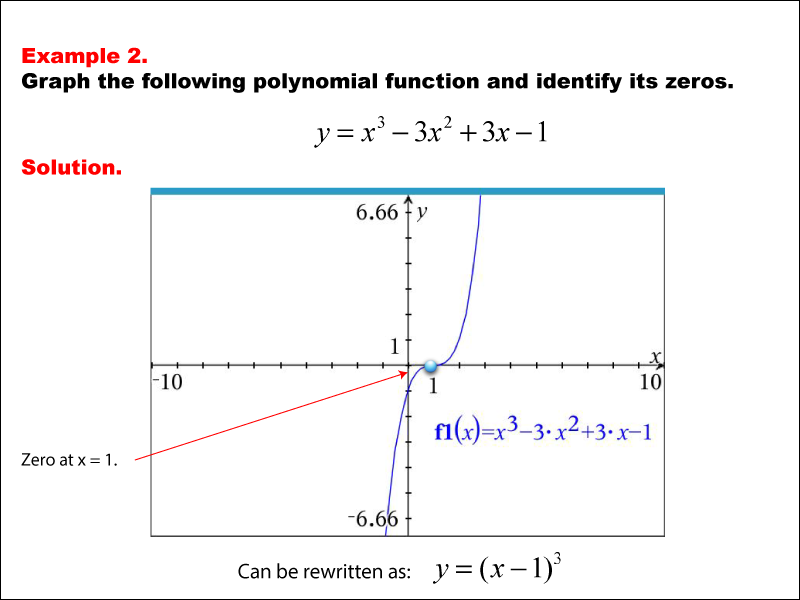
The graph represents the cubic function y = x3 - 3x2 + 3x - 1. The curve touches and crosses the x-axis at x = 1, indicating a zero at this point. Example 2: The caption reads 'Graph the following polynomial function and identify its zeros.' The equation is y = x3 - 3x2 + 3x - 1, and the solution shows a zero at x = 1. The function can be rewritten as y = (x - 1)3.
Polynomial functions, particularly cubic and quartic polynomials, exhibit different behaviors based on their structure. By graphing these functions, students can see how coefficients and terms affect the shape and zeros of the graph. These examples help students connect the algebraic expression of a polynomial to its graphical representation, reinforcing their understanding of concepts like zeros, symmetry, and end behavior.
Seeing multiple worked-out examples is essential for students to fully understand polynomial functions. Each example illustrates different characteristics—like where the graph crosses the x-axis and how the shape varies—helping students recognize patterns and anticipate behaviors in similar functions.
Teacher’s Script: Take a look at this polynomial function. Notice where the graph intersects the x-axis—that’s where the zeros are located. In this example, the polynomial shows a unique structure that determines its graph's shape. As you analyze this, think about how changes in each term affect the graph's behavior and position.
For a complete collection of math examples related to Graphs of Polynomial Functions click on this link: Math Examples: Graphs of Polynomial Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.APR.B.3, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.IF.C.7.C |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Polynomials • Polynomial Functions and Equations |
| Copyright Year | 2020 |
| Keywords | polynomial functions |