edcom-728x90

IXL Ad

Math Example--Polynomial Concepts--Pascal's Triangle: Example 1
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Polynomials >> Polynomial Expressions

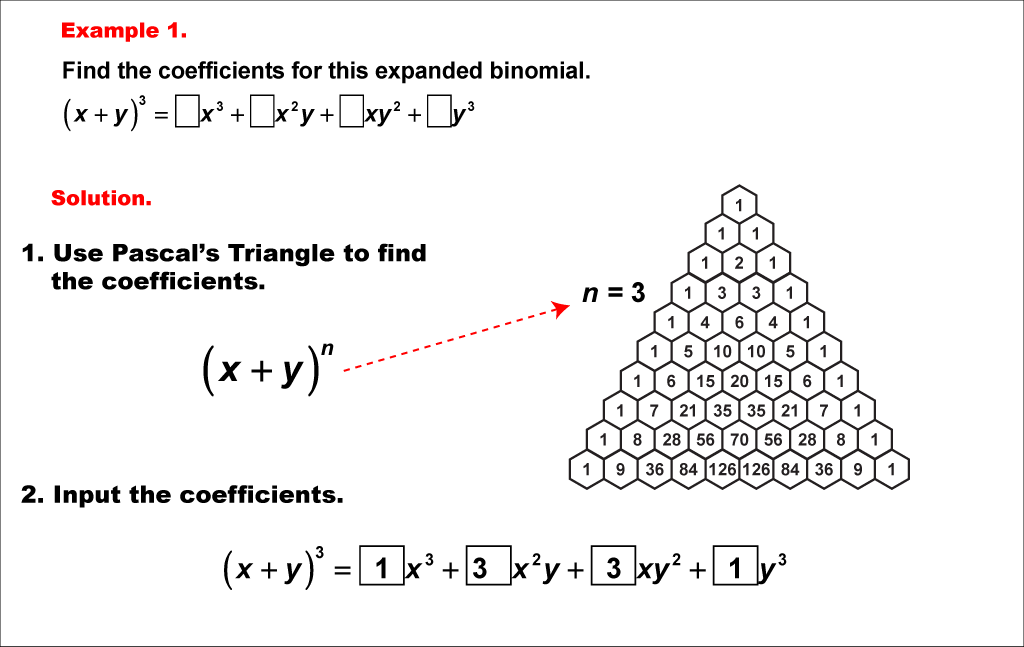
Math Example--Polynomial Concepts--Pascal's Triangle: Example 1

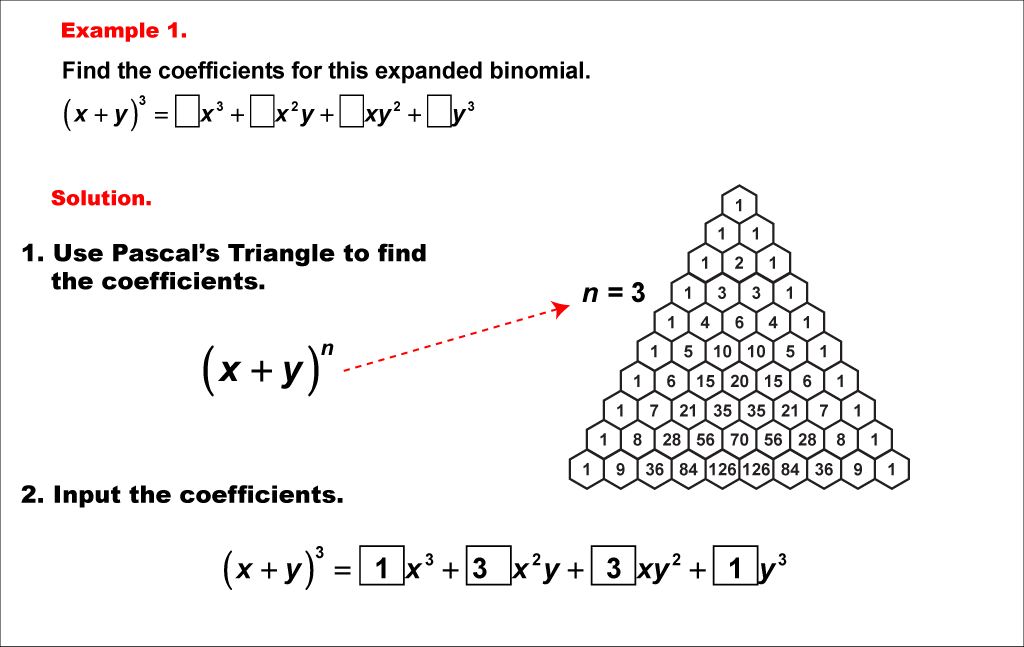
Math Example--Polynomial Concepts--Pascal's Triangle: Example 1

This is part of a collection of math examples that focus on polynomial concepts. This includes adding, subtracting, multiplying, and dividing polynomials, along with polynomial properties.

To see the complete math example collection on this topic, click on this link

Note: The download is an image file.

Related Resources

To see additional resources on this topic, click on the Related Resources tab.

Create a Slide Show

Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To learn more about Slide Show Creator, click on this Link: 

Accessibility

This resource can also be used with a screen reader. Follow these steps.

  • Click on the Accessibility icon on the upper-right part of the screen.

  • From the menu, click on the Screen Reader button. Then close the Accessibility menu.

  • Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.

Common Core Standards CCSS.MATH.CONTENT.HSA.APR.C.5
Grade Range 8 - 10
Curriculum Nodes Algebra
    • Polynomials
        • Polynomial Expressions
Copyright Year 2021
Keywords Pascal's Triangle, binomial expansion