Display Title
Math Example--Polynomial Concepts--Pascal's Triangle: Example 2
Display Title
Math Example--Polynomial Concepts--Pascal's Triangle: Example 2
Topic
Polynomials
Description
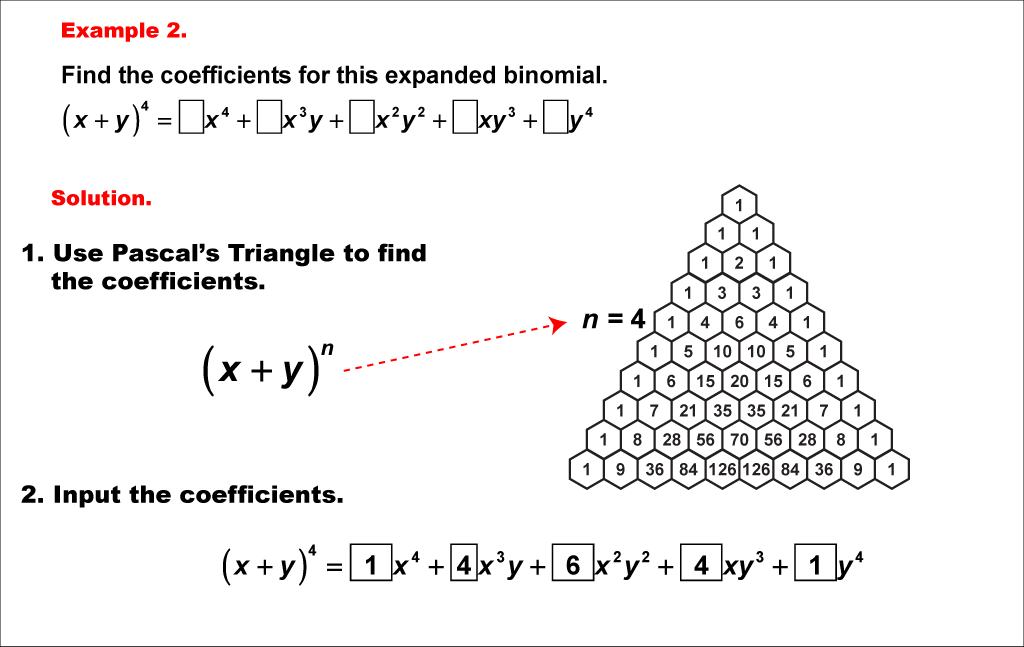
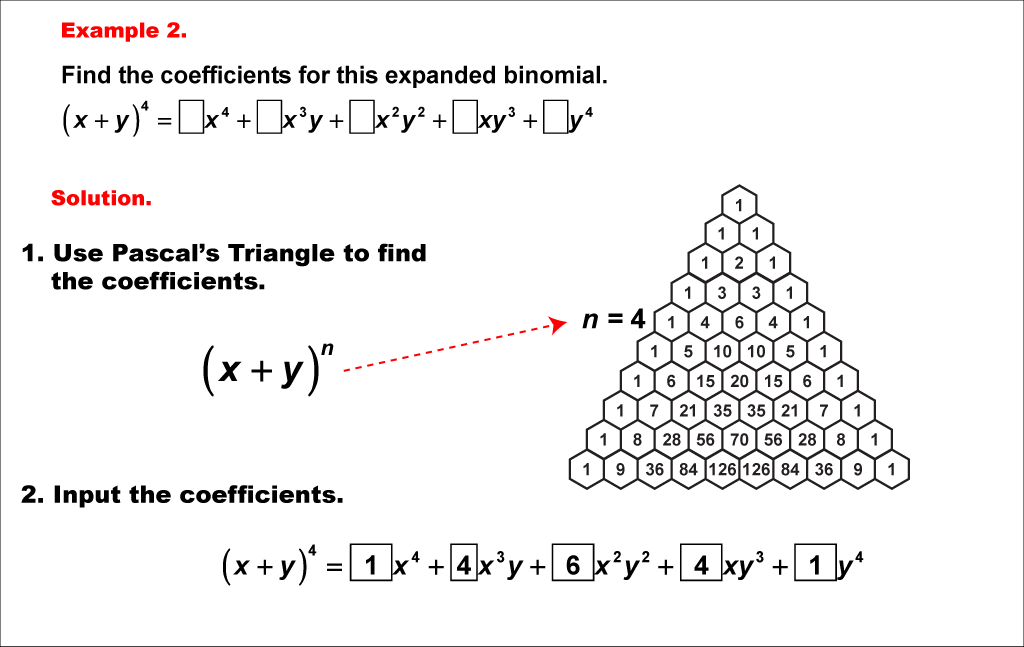
This example explores the binomial expansion of (x + y)4 using Pascal's Triangle. We aim to find the coefficients for the expanded expression (x + y)4 = _x4 + _x3y + _x2y2 + _xy3 + _y4, where the blanks represent the coefficients we need to determine.
Pascal's Triangle serves as an elegant and efficient method for generating coefficients in binomial expansions. Each row of the triangle corresponds to the coefficients of a specific power of a binomial expression. For this example, we focus on the fifth row of Pascal's Triangle (n = 4) to obtain the sequence 1, 4, 6, 4, 1, which provides the coefficients for our expansion.
Examining various examples of binomial expansions is essential for students to fully grasp the concept. By working through different powers and observing the resulting patterns, students develop a more comprehensive understanding of algebraic structures and combinatorial principles. These examples reinforce the symmetry and predictability inherent in mathematical patterns, helping students build confidence in their ability to work with more complex polynomial expressions.
Teacher's Script: Now, let's look at the expansion of (x + y)4. Can you see how Pascal's Triangle makes finding these coefficients so much easier? We'll use the row corresponding to n = 4, which gives us 1, 4, 6, 4, 1. Watch how we apply these to our expression: (x + y)4 = _x4 + _x3y + _x2y2 + _xy3 + _y4. Notice the symmetry in the coefficients -- isn't that interesting?
For a complete collection of math examples related to Polynomials click on this link: Math Examples: Pascal's Triangle Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.APR.C.5 |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Polynomials • Polynomial Expressions |
| Copyright Year | 2021 |
| Keywords | Pascal's Triangle, binomial expansion |