Display Title
Math Example--Polynomial Concepts--Synthetic Division--Example 03
Display Title
Math Example--Polynomial Concepts--Synthetic Division--Example 03
Topic
Polynomials
Description
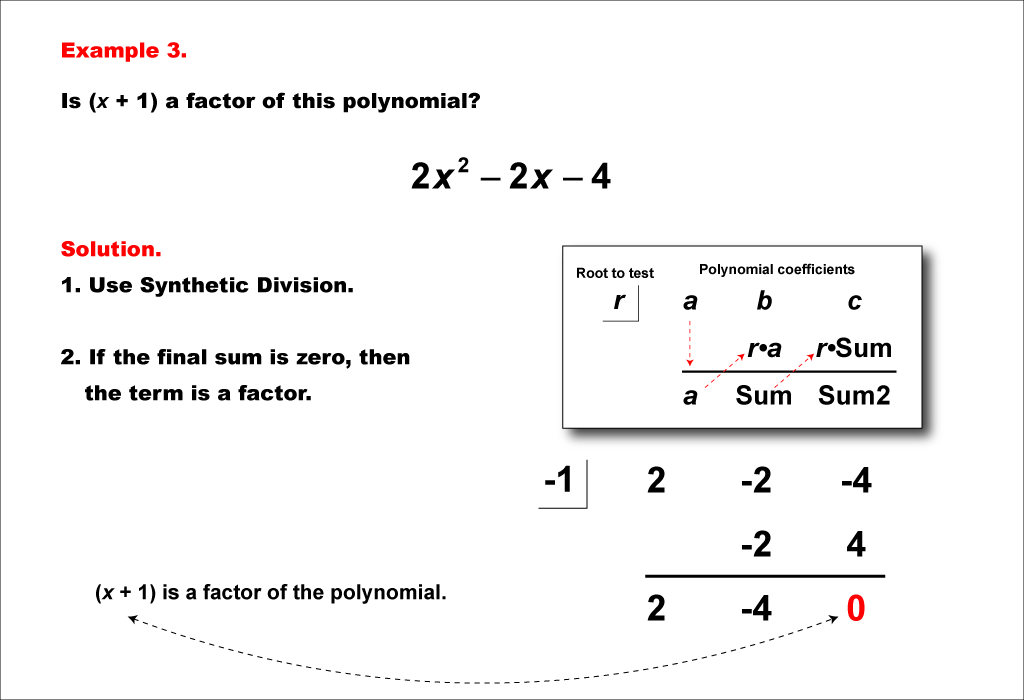
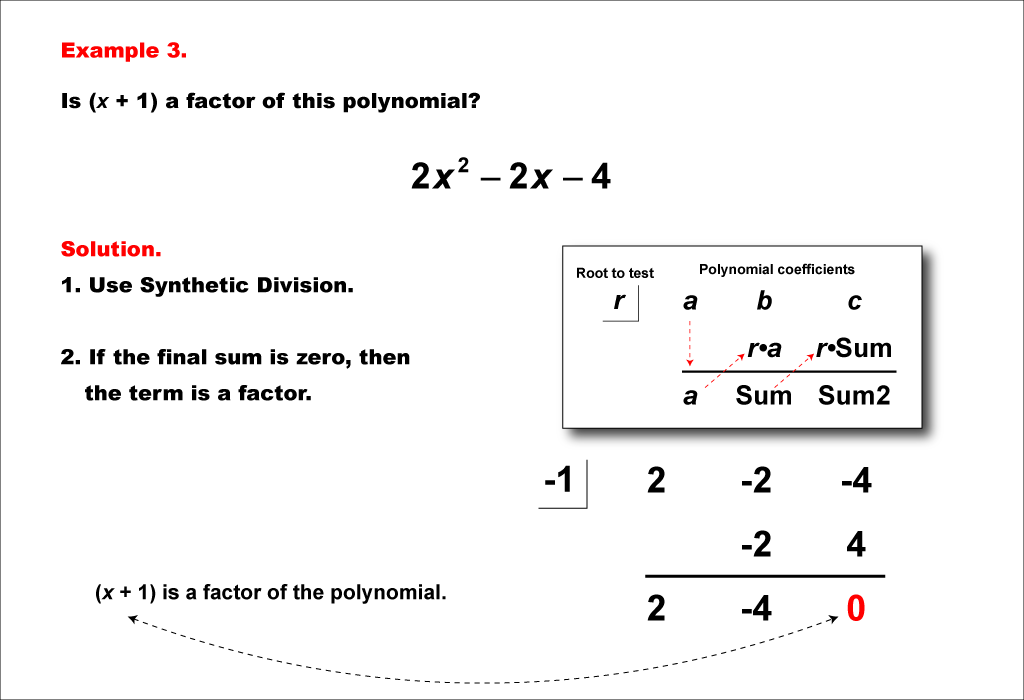
Determine if x+1 is a factor of the polynomial 2x2 - 2x - 4. Use synthetic division with x = -1. The polynomial coefficients are 2, -2, and -4. After performing synthetic division, the final remainder is 0, confirming that x+1 is a factor of 2x2 - 2x - 4.
The topic of synthetic division is explored here, which is a simplified way to divide polynomials, often used when the divisor is in the form (x - a). These examples showcase how synthetic division allows for faster computations compared to traditional polynomial division. By using synthetic division, students see a step-by-step approach to finding factors of polynomials, which reinforces their understanding of polynomial functions and factorization.
Seeing multiple worked-out examples is crucial for students to fully grasp synthetic division. It allows them to observe the pattern in computations and how each step builds toward simplifying a polynomial division problem. This reinforces their procedural skills and helps them recognize common errors.
Teacher’s Script: Let's examine how synthetic division works with this example. Look at the divisor and set it up to divide our polynomial. Follow each step to see how coefficients change as we progress through the division. This helps you identify the remainder and whether the divisor is a factor of the polynomial.
For a complete collection of math examples related to Polynomials click on this link: Math Examples: Synthetic Division Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.APR.B.3, CCSS.MATH.CONTENT.HSA.APR.B.2 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Polynomials • Polynomial Expressions • Polynomial Functions and Equations |
| Copyright Year | 2021 |
| Keywords | polynomials |