Display Title
Math Example--Quadratics--Conic Sections: Example 14
Display Title
Conic Sections: Example 14
Topic
Quadratics
Description
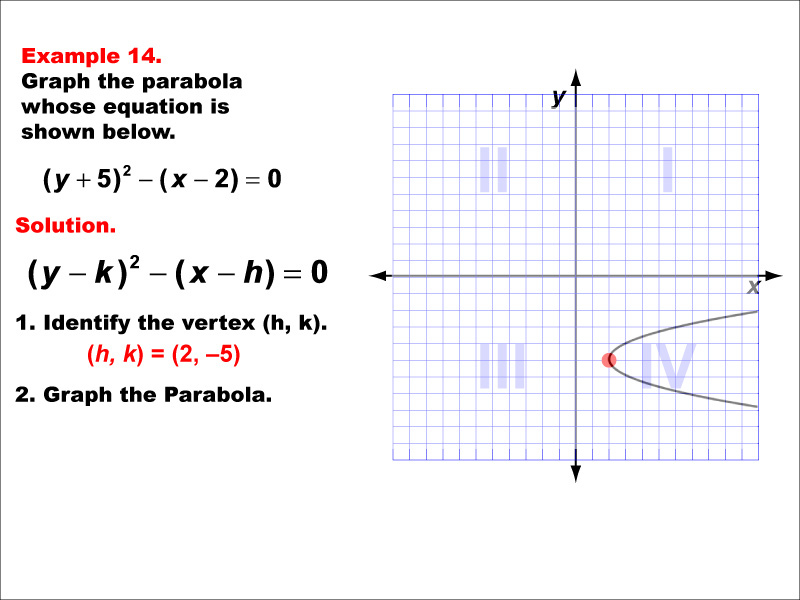
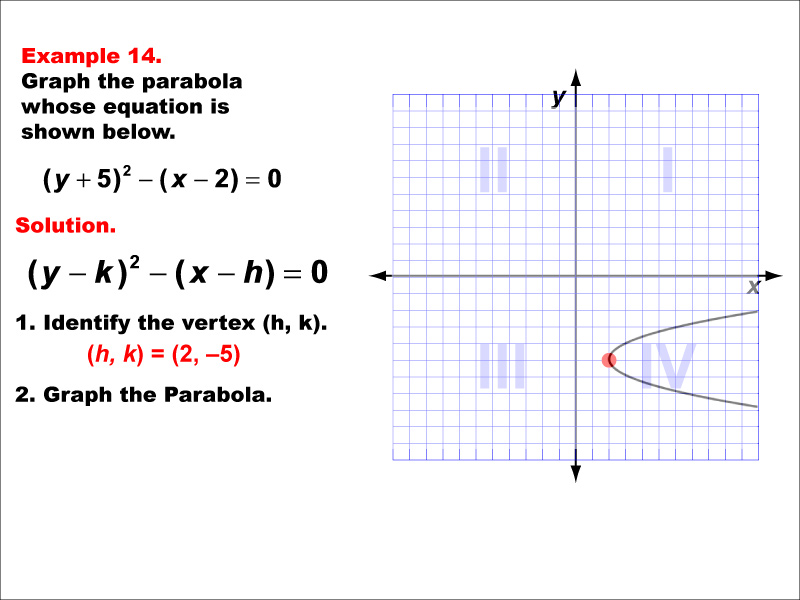
This example shows a horizontal parabola opening to the right, with its vertex in the fourth quadrant. The equation would be x = a(y - k)² + h, where 'a' is positive, and (h, k) represents the coordinates of the vertex. This example is particularly useful for demonstrating how the parabola's shape and position are affected when the vertex is in different quadrants. It reinforces the understanding of transformations applied to the basic parabola equation and how these transformations are reflected in the graph. As a conic section, this parabola exemplifies the rich interplay between algebra and geometry, which is fundamental to many areas of mathematics and its applications.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |