Display Title
Math Example--Quadratics--Conic Sections: Example 16
Display Title
Math Example--Quadratics--Conic Sections: Example 16
Conic Sections: Example 16
Topic
Quadratics
Description
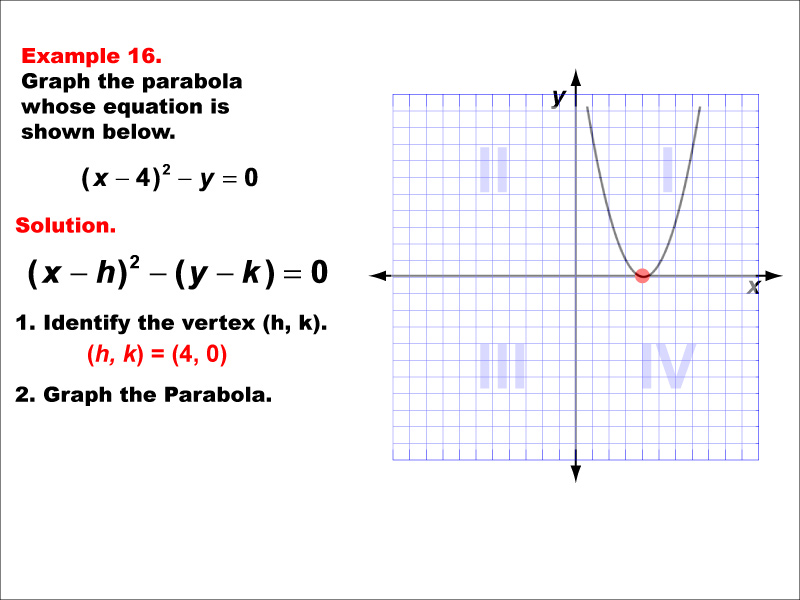
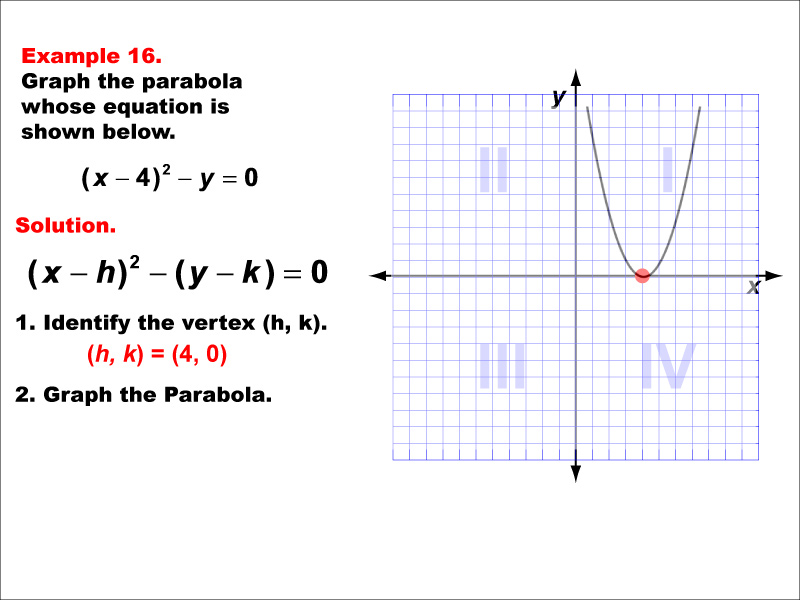
This example shows a vertically aligned parabola opening upward. The general form of its equation is y = a(x - h)² + k, where (h, k) is the vertex and 'a' is positive. The vertexis on the x-axis, which somewhat simplifies the equation. This parabola demonstrates how the position of the vertex affects the graph's location. Vertical parabolas are functions, as each x-value corresponds to a single y-value. Understanding these parabolas is crucial for modeling many real-world phenomena, such as projectile motion or optimization problems in economics.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |