Display Title
Math Example--Quadratics--Conic Sections: Example 18
Display Title
Conic Sections: Example 18
Topic
Quadratics
Description
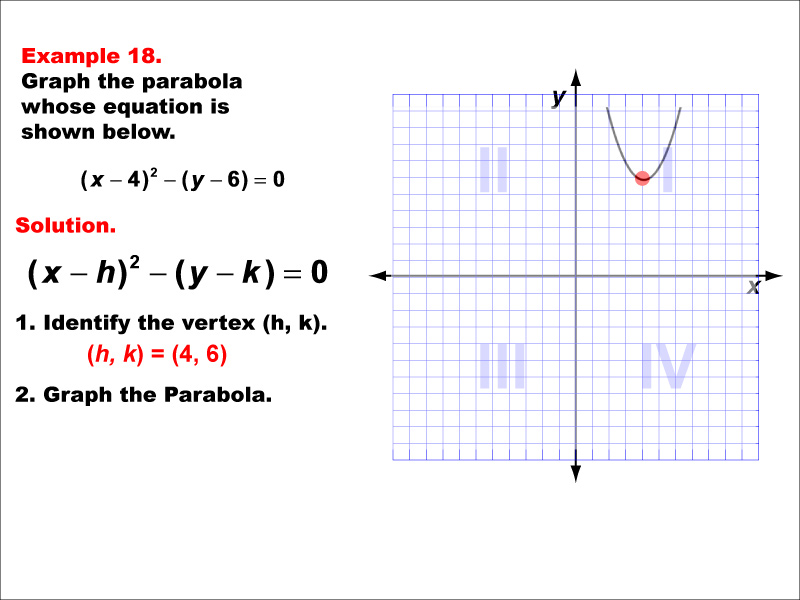
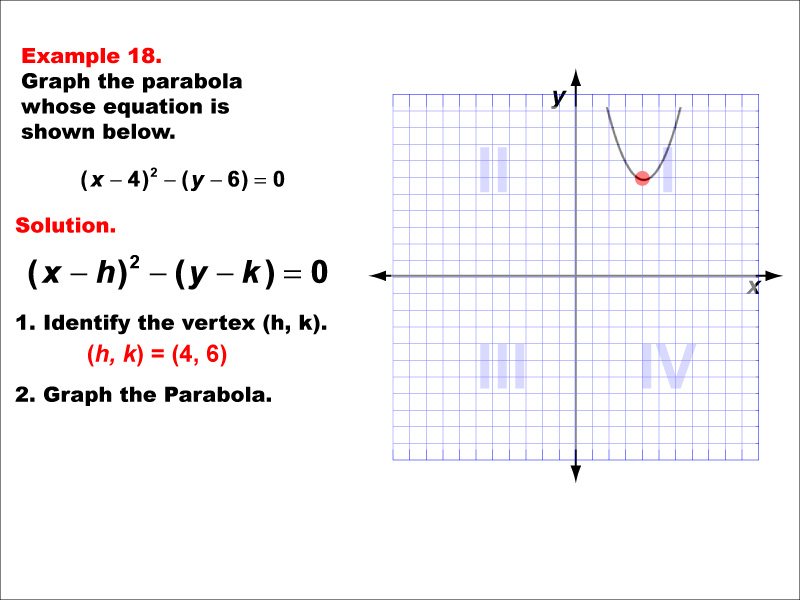
This example shows a vertically aligned parabola opening upward. The general form of its equation is y = a(x - h)² + k, where (h, k) is the vertex and 'a' is positive. A negative sign before 'a' would cause the parabola to open downward. The vertex is in the first quadrant. This parabola demonstrates how the position of the vertex and the sign of 'a' affect the graph's location and orientation. Vertical parabolas are functions, as each x-value corresponds to a single y-value. This type of parabola is often used to model situations with a maximum value, such as the height of a projectile or revenue in certain economic models.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |