Display Title
Math Example--Quadratics--Conic Sections: Example 2
Display Title
Conic Sections: Example 2
Topic
Quadratics
Description
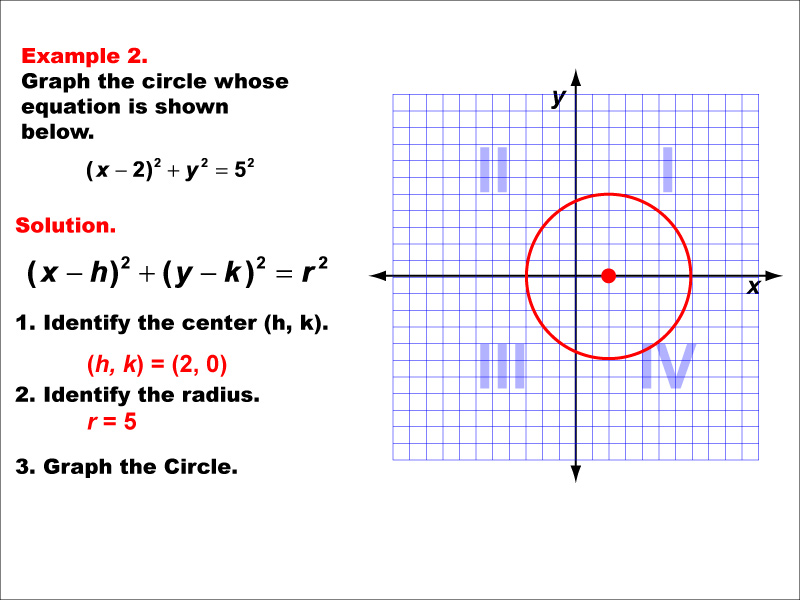
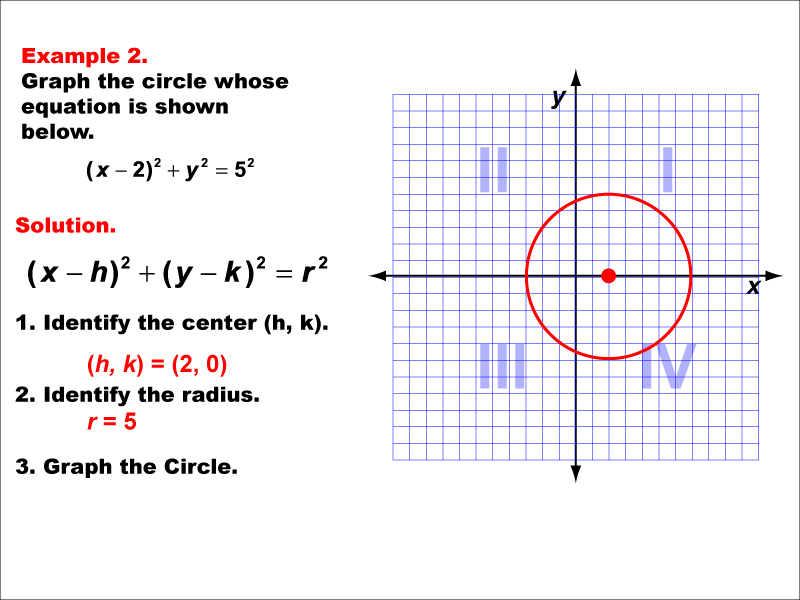
This example illustrates another circle, but with its center shifted from the origin. The equation likely takes the form (x - h)² + (y - k)² = r², where (h, k) is not (0, 0). This demonstrates how the general equation of a circle can be translated to different positions on the coordinate plane. Understanding these translations is key to grasping transformations of functions and conic sections. It's worth noting that despite the shift, the circle maintains its fundamental property of equidistance from the center point to any point on its circumference. This example reinforces the concept that conic sections, including circles, are not always centered at the origin and can be moved around the coordinate plane.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |