Display Title
Math Example--Quadratics--Conic Sections: Example 21
Display Title
Math Example--Quadratics--Conic Sections: Example 21
Conic Sections: Example 21
Topic
Quadratics
Description
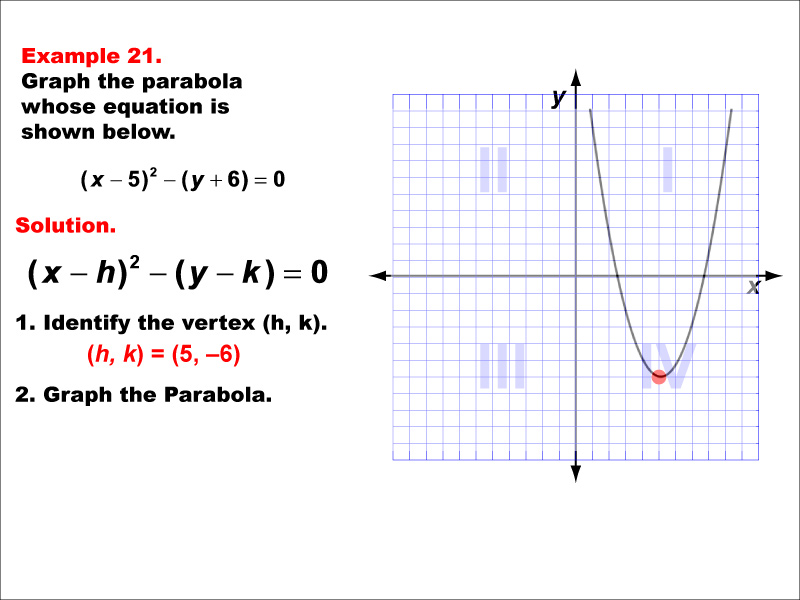
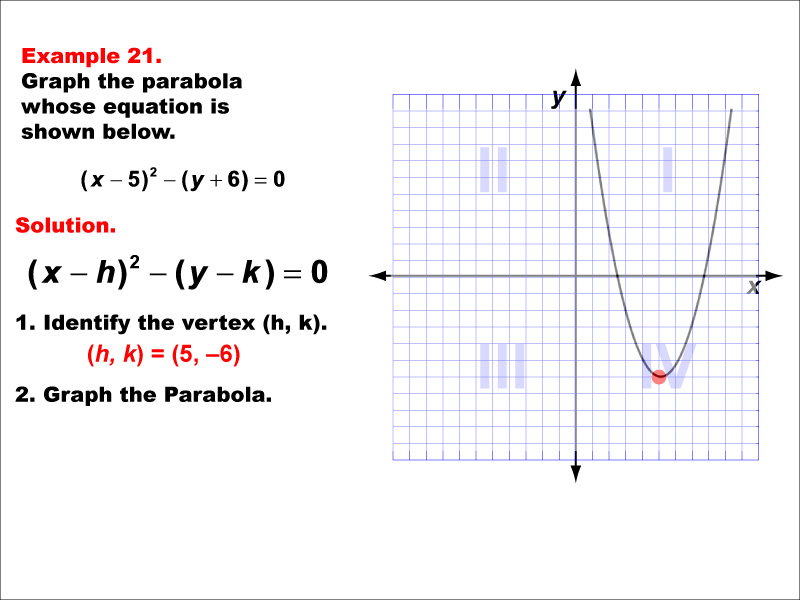
This example depicts a vertically aligned parabola opening upward, with its vertex in the fourth quadrant. The equation would be y = a(x - h)² + k, where 'a' is positive, and (h, k) represents the coordinates of the vertex. This example is valuable for understanding how the signs in the equation affect the orientation and position of the parabola. It reinforces the concept of transformations applied to the basic quadratic function y = x². Parabolas like this are used in various fields, including optics for designing reflective surfaces and in architecture for creating aesthetically pleasing arches.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |