Display Title
Math Example--Quadratics--Conic Sections: Example 27
Display Title
Conic Sections: Example 27
Topic
Quadratics
Description
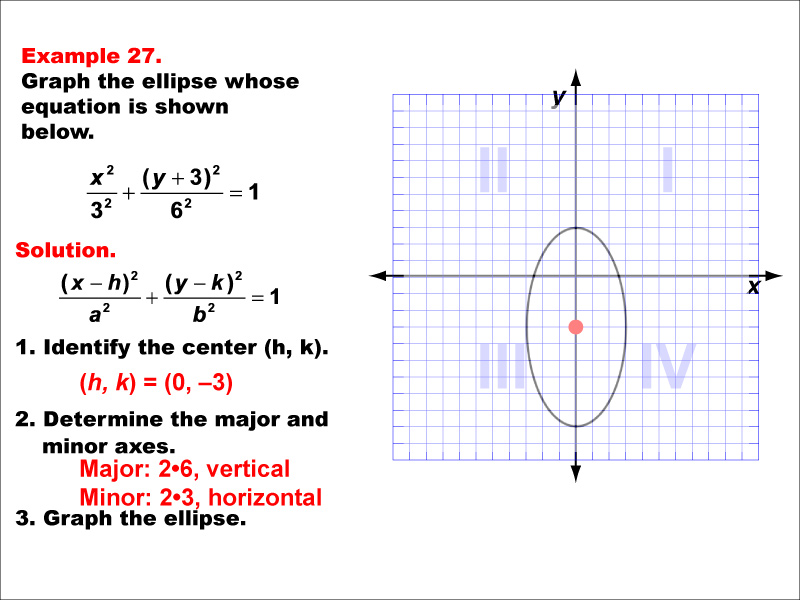
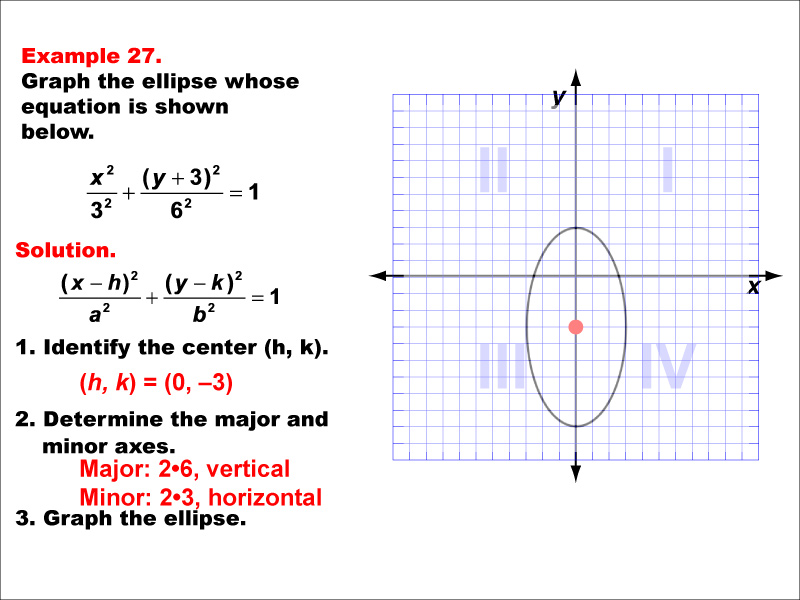
This example shows an ellipse with its center not at the origin. The general equation of an ellipse is ((x-h)²/a²) + ((y-k)²/b²) = 1, where (h,k) is the center and a and b are the lengths of the semi-major and semi-minor axes. In this case, the ellipse is vertically oriented with its center on the y-axis. The specific equation might be something like (x²/9) + ((y + 3)²/36) = 1. This example demonstrates how translating the center affects the equation of the ellipse while maintaining its basic shape and orientation. It highlights the versatility of conic sections in representing various shapes and positions in the coordinate plane.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |