Display Title
Math Example--Quadratics--Conic Sections: Example 35
Display Title
Math Example--Quadratics--Conic Sections: Example 35
Conic Sections: Example 35
Topic
Quadratics
Description
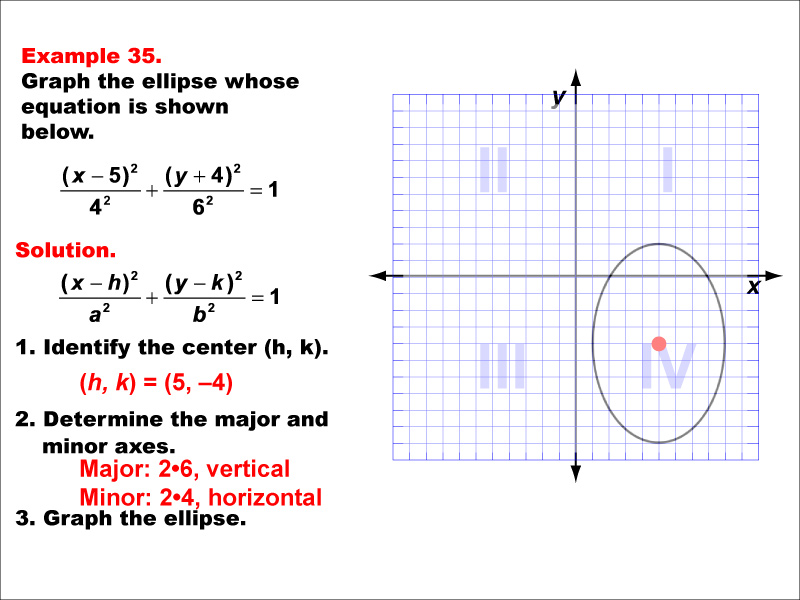
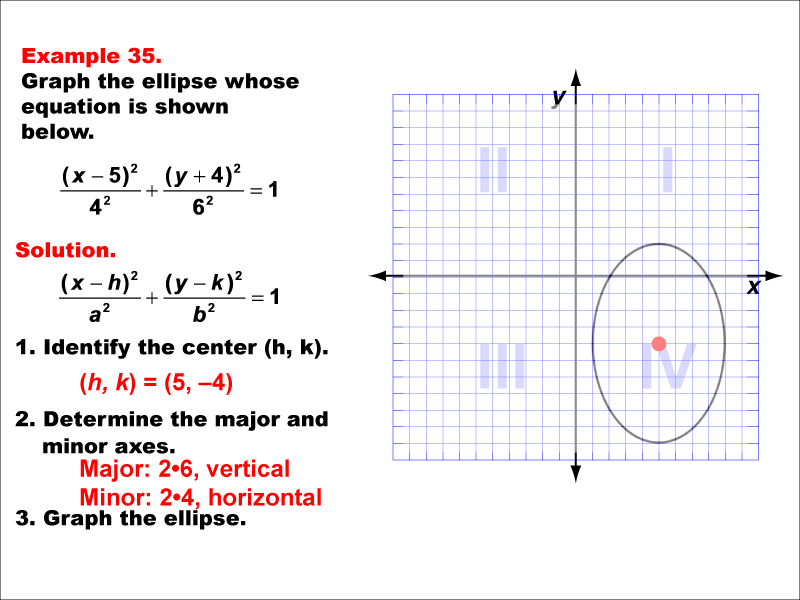
This example shows an ellipse with its center not at the origin. The equation is of the form ((x - h)²/a²) + ((y - k)²/b²) = 1, where (h, k) is the center. The ellipse is vertically oriented with its center in the fourth quadrant. The equation is ((x - 5)²/16) + ((y + 4)²/36) = 1. This example demonstrates how the position of the center and the relative sizes of a and b affect the shape and orientation of the ellipse. It's a good illustration of how the general equation of an ellipse can represent a wide variety of elliptical shapes in different positions on the coordinate plane.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |