Display Title
Math Example--Quadratics--Conic Sections: Example 4
Display Title
Conic Sections: Example 4
Topic
Quadratics
Description
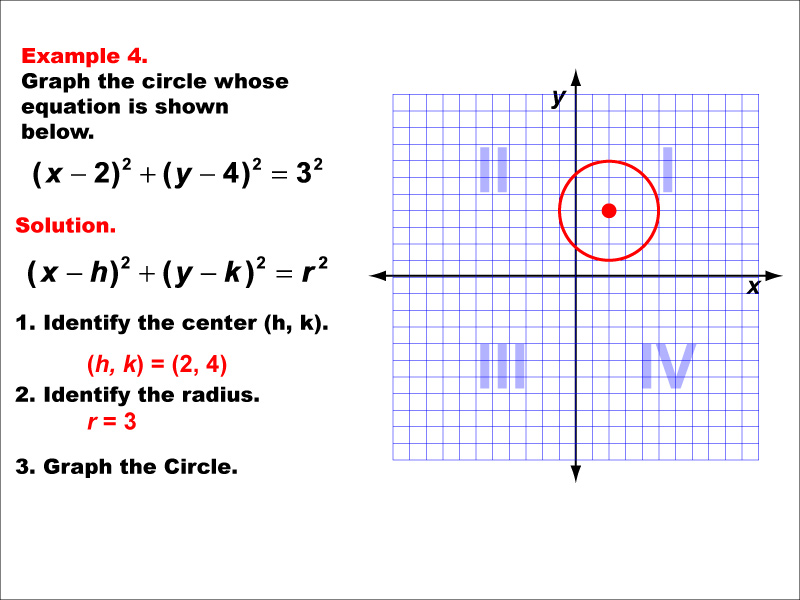
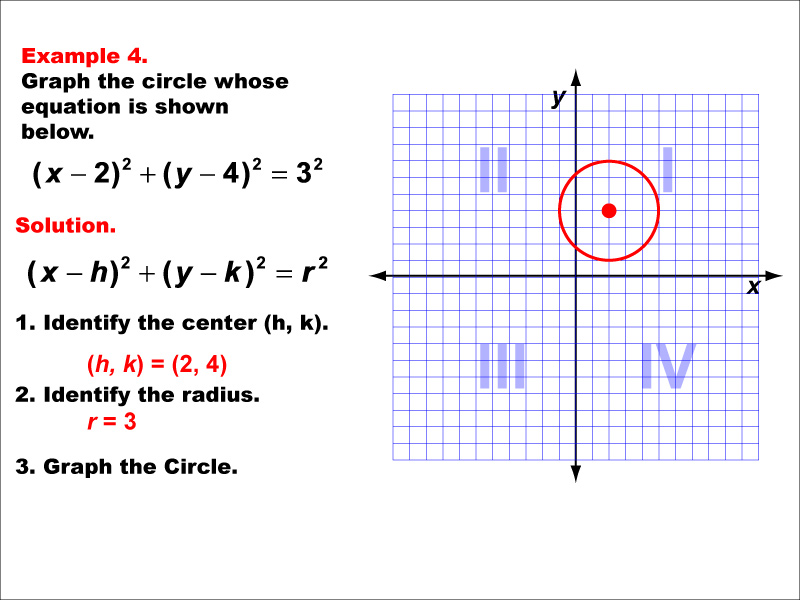
This example showcases a circle, a fundamental conic section. The equation of a circle is (x - h)² + (y - k)² = r², where (h, k) is the center and r is the radius. This circle is centered at a point other than the origin, (2, 4), with a radius of 3 units. Circles are unique among conic sections as they have a constant distance from a central point to any point on the circumference. This example demonstrates how shifting the center affects the equation and graph of a circle. It's important to note that while circles are conic sections, they are not functions as they fail the vertical line test. Understanding circles is crucial in many fields, including geometry, physics, and engineering.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |