Display Title
Math Example--Quadratics--Conic Sections: Example 6
Display Title
Conic Sections: Example 6
Topic
Quadratics
Description
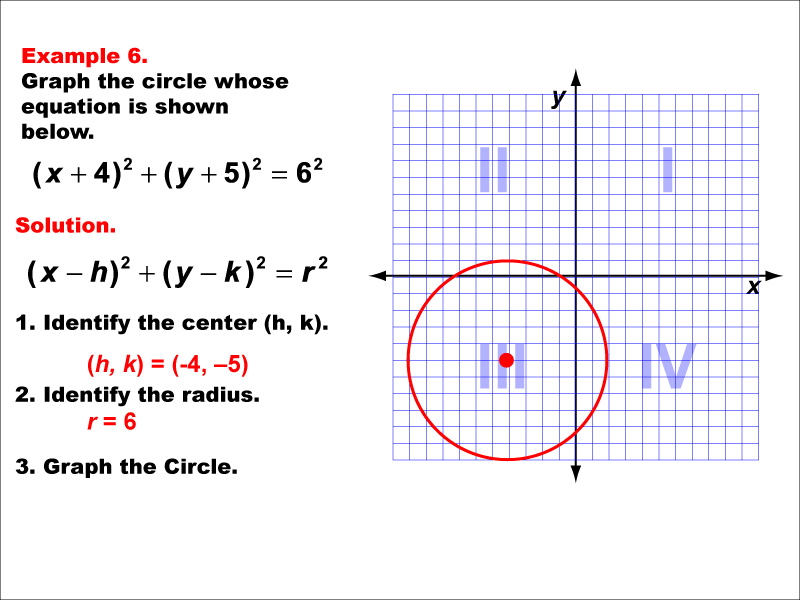
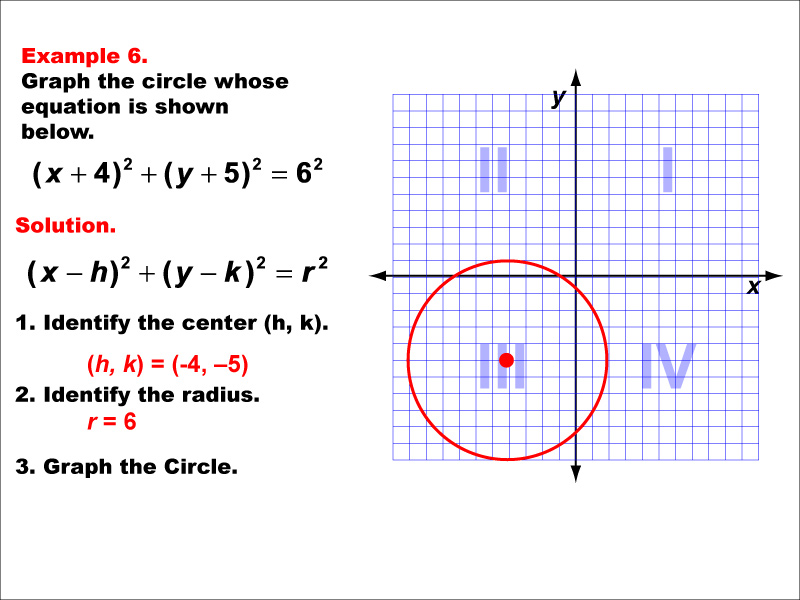
This example illustrates a circle with its center at (-4, -5). The equation for this circle would be (x - h)² + (y - k)² = r², where r is the radius, which is 6 units. This standard form of a circle centered at the origin is a special case that simplifies many calculations. It demonstrates the symmetry of circles around their center point. Learning about this basic form of a circle equation is fundamental to understanding more complex transformations and properties of circles. As with all circles, this example reinforces the concept that conic sections are not always functions, as a vertical line would intersect the circle at two points (except at the y-axis).
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |