Display Title
Math Example--Quadratics--Conic Sections: Example 7
Display Title
Conic Sections: Example 7
Topic
Quadratics
Description
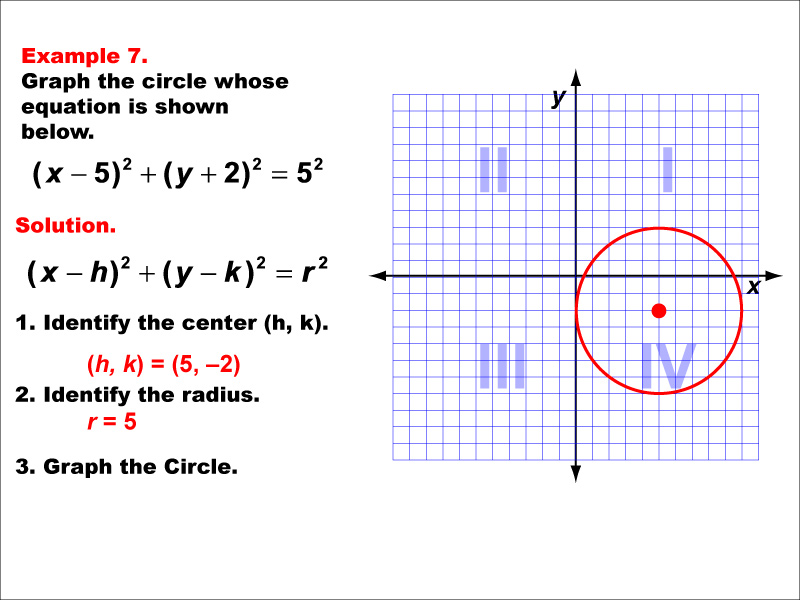
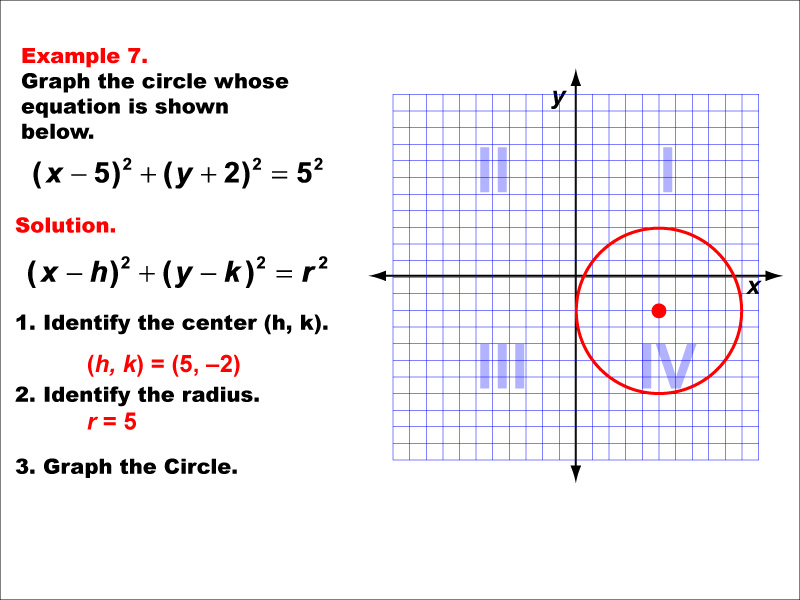
This example shows a circle with its center in the fourth quadrant, at (5, -2), and a radius of 5 units. The equation would be (x - 5)² + (y + 2)² = 25. This example demonstrates how the general form of a circle equation (x - h)² + (y - k)² = r² can be used to graph circles in any position on the coordinate plane. It highlights the importance of understanding coordinate translations in conic sections. The circle's position reinforces the concept of how changing the h and k values in the equation affects the circle's location. As with all circles, this example is not a function, emphasizing the distinction between conic sections and functions.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |