Display Title
Math Example--Quadratics--Conic Sections: Example 8
Display Title
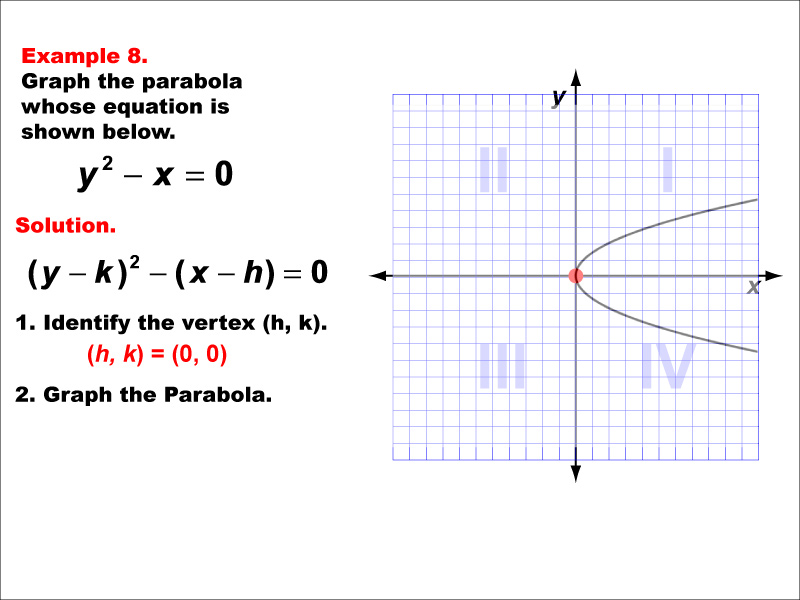
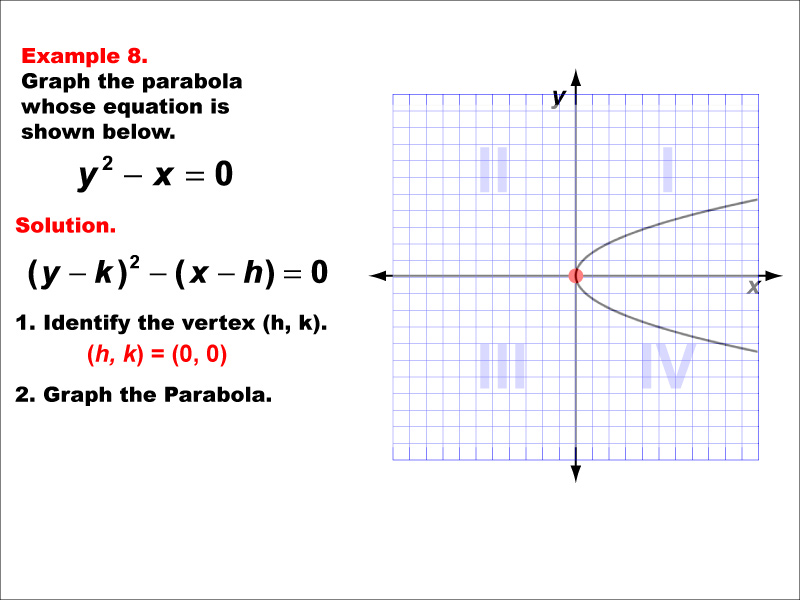
Conic Sections: Example 8
Topic
Quadratics
Description
This example shows a horizontal parabola opening to the right. The general form of its equation is x = a(y - k)² + h, where (h, k) is the vertex and 'a' is positive. In this case, the vertex is at the origin. Horizontal parabolas are not functions as they fail the vertical line test. This example demonstrates how parabolas, as conic sections, can have different orientations. Parabolas are important in fields like physics (projectile motion) and engineering (reflector design). Conic sections, including parabolas, ellipses, circles, and hyperbolas, are fundamental in mathematics and have numerous real-world applications, from planetary orbits to satellite dishes.
For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.A.1, CCSS.MATH.CONTENT.HSG.GPE.A.2, CCSS.MATH.CONTENT.HSG.GPE.A.3 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Conic Sections |
| Copyright Year | 2013 |
| Keywords | conic section, quadratic relations |